3 输入文件、输出文件介绍¶
3.1 核心输入文件PASP.input¶
3.1.1 PASP.input文件读取规则¶
PASP软件的核心输入文件是 PASP.input ,一般在该文件中选定所用的功能模块,并提供研究对象的结构信息、设置相应的参数等;另外,对于某些功能模块,可能还需要其他的补充输入文件。所有的输入文件都应在同一文件夹下,并在相应的文件夹内调用PASP软件(调用方法参见1.2节)。
在 PASP.input 文件中将逐行读取内容。每行开头的若干空格和制表符(由Tab键生成)忽略不计,每行内的字符串(包括数据)之间由任意数量(但不少于一个)的空格或制表符隔开。
当某行的第一个字符串为软件指定的若干关键词(例如NumberOfAtoms等,不区分大小写)之一时,该行内容有效。例如,若某行内容为“ numberofatoms 5 ”,则该行内容有效。
当某行第一个字符串为 “%block” 时,将会读取该行的第二个字符串(记为strA),这里要求第二个字符串必须是软件制定的若干block类型的关键词(例如SuperCell,fig.mdist等,不区分大小写)之一;这时软件将会连续读取多行内容,由“ %block strA ”开始,到“ %endblock strA ”结束。不同的关键词内容之间可以空任意行;但是block类型内容的内部不能随意空行,必须严格按照该block的格式填写内容。
井号(#)可用于备注信息,每行井号之后的内容不被软件读取。例如,若某行内容为“ NumberOfAtoms 5#total ”,则该行的内容仍然是有效的,并且等价于“ NumberOfAtoms 5 ”。为了输入文件的美观与可读性,建议井号和有效的内容之间用若干空格或制表符隔开,例如“ NumberOfAtoms 5 #total ”。
可以在 PASP.input 中用“ %include 文件名 ”的格式添加其他输入文件。软件在读到该行内容时,会跳到相应的文件继续逐行读取,读完相应文件的内容后再回到“ %include 文件名 ”的位置继续读取后面的内容。常用此格式添加的文件名包括“ cell.str ”、“ unit_cell.str ”和“ MC.input ”等,在本手册中我们称这些文件为( PASP.input 的)附属文件。这些额外添加的文件的内容格式与 PASP.input 一致。原则上可以将这些额外添加的输入文件的内容全部移到 PASP.input 文件中,而在 PASP.input 文件中删掉所有以“ %include ”开头的行(如需保证移动内容前后的设置完全等效,可将移动的内容放置在之前写“ %include 文件名 ”的相应位置)。
若同一关键词在 PASP.input 及其通过“ %include 文件名 ”调用的文件中出现两次或以上时,仅第一次出现关键词时对应的内容有效。这是因为软件在需要读取某项信息时,会在 PASP.input 及其调用文件中逐行搜索相应关键词,并且在首次发现关键词后停止继续搜索。例如,在 PASP.input 中出现“ Model Invariant ”和“ %include MC.input ”,并且在 MC.input 中出现“ Model atomic_effective_H ”时,哪个“ Model ”设置行起作用取决于 PASP.input 中“ Model Invariant ”和“ %include MC.input ”的先后顺序:若“ %include MC.input ”出现在前,则软件会先读到 MC.input 中的“ Model atomic_effective_H ”,于是“ Model atomic_effective_H ”起作用,而“ Model Invariant ”无效;反之则效果相反。
为布尔型(boolean)变量赋值时,取True值时可写成“T”或“.TRUE.”,取 False 值时可写成“F”或“.FALSE.”,为简便起见,案例中均采用“T”或“F”的形式。
以下3.1.2节将介绍 PASP.input 中最常用的几个设置项,它们在多个不同模块中都可能会用到。另外还有一些常用的设置项经常以“ %include 文件名 ”的方式写在附属文件中,包括“ cell.str ”、“ unit_cell.str ”、“ MC.input ”和“ MD.input ”等文件,这些将在3.1.3至3.1.6节介绍。3.1.7节及之后的各小节将补充介绍各个功能模块下常用的设置项。
3.1.2 最常用设置项¶
本节介绍输入文件 PASP.input 中最常用的一些设置项,这些设置项在大多数功能模块(主要由Model设置项决定)中都会用到。软件中实际要用到哪些设置项主要取决于功能模块的选择。
3.1.2.1 Model¶
参数名称: Model
默认值: Charge_ordering
选值: find_J_path_sym/Invariant/Spin_lattice_interaction/atomic_effective_H/GA/TB/KNB/magnon(这里仅列出本手册涉及的选项)。
描述: 这是PASP软件最重要的一项设置,它决定了软件使用哪个功能模块,这通常决定了软件读取哪些设置项。因此建议将该设置放在足够醒目的位置,比如第一行。
案例:
Model find_J_path_sym
3.1.2.2 block SuperCell¶
参数名称: block SuperCell
默认值: 不扩胞(1×1×1胞)
可选值: 3×3可逆矩阵,矩阵元为整数。
描述: 常用设置。提供扩胞信息,扩胞时以 cell.str 文件(参见3.1.3节)提供的结构信息为基础。在本软件中,我们习惯上称 cell.str 提供的结构为晶胞(即使它可能并不是晶胞),而用“
block SuperCell”生成的胞为超胞。案例中为2×2×2扩胞。案例:
%block SuperCell 2 0 0 0 2 0 0 0 2 %endblock SuperCell
3.1.2.3 block Z_values¶
参数名称: block Z_values
默认值: 缺省时根据“%block AtomicCoordinatesAndAtomicSpecies”(参见3.1.3.6节)的第五列所提供元素名称自动设定;若仍缺失相应数据,则全部赋值为1。
可选值: 有效的原子序数。
描述: 常用设置。提供各元素的原子序数,顺序应当按照 cell.str 文件(参见3.1.3节)提供原子坐标时各元素出现的先后顺序(这样 cell.str 文件中元素编号才能与“
block Z_values”的信息正确匹配)。案例以 \(BiFeO_{3}\) 为例。
备注
在TB模块中, Z_values 应取每个元素所考虑轨道的电子数,而非元素的原子序数。
案例:
%block Z_values 83 26 8 %endblock Z_values
3.1.2.4 block isaAB¶
参数名称: block isaAB
默认值: 缺省时两个数都赋值为0。
可选值: 0或原子编号。
描述: 常用设置。需提供两个整数,指出研究哪两种元素之间的相互作用。两个整数代表相互作用的两种元素的编号(即在“block Z_values”中的排序)。案例以 \(BiFeO_{3}\) 为例,需考虑Fe元素之间的磁相互作用,该元素在“block Z_values”中排第二位,因此填“2 2”。
案例:
%block isaAB 2 2 %endblock isaAB
3.1.2.5 自旋大小与外磁场设置¶
参数名称: block Spin_values
默认值: 缺省时全部赋值为1。
可选值: 非负实数。
描述: 常用设置。常提供各元素原子的电子总自旋量子数的二倍,常取整数(因为总自旋量子数为半整数);在采用自旋矢量归一化模型时,需将磁性原子的对应值设为2。通常原子磁矩 \(\boldsymbol{\mu}\) 主要由局域于过渡元素原子的d或f轨道电子的总自旋磁矩 \(\boldsymbol{\mu}_S\) 决定,近似满足
其中 \(\mu_B= |e| \hbar /(2 m)\) 为玻尔磁子(Bohr magneton),\(\boldsymbol{S}\) 为局域于原子的电子的总自旋矢量,其模长为电子的总自旋量子数。所以这里“ block Spin_values ”所提供的值也可以理解为原子磁矩的近似大小 \({\mu}_B\) (以为单位)。
备注
在有效自旋哈密顿量方法中(例如“ Model Invariant ”以及相应的蒙特卡洛模拟模块“ Model atomic_effective_H ”),经常假定自旋为1(自旋矢量归一化),从而使所有相互作用系数的单位均为能量单位(PASP软件中一般取eV单位)。当假定自旋为1时,这里的整数应为其二倍,即取2,此时原子磁矩假定为2 \({\mu}_B\)。
案例以 \(BiFeO_{3}\) 为例,仅Fe元素具有非零的自旋量子数,其磁矩大小约为3 \({\mu}_B\),因此可写成案例1形式;若采用自旋矢量归一化模型,则写成案例2形式。
案例1:
%block Spin_values 0 3 0 %endblock Spin_values
案例2(自旋矢量归一化模型):
%block Spin_values 0 2 0 %endblock Spin_values
参数名称: block ExternalMagneticField
默认值: 缺省时全部赋值为0。
可选值: 实数。
描述: 该设置项在蒙特卡洛模拟(以及CG局域优化)中可能用到,用于添加外磁场,单位T。由于在蒙特卡洛模拟阶段才用到,所以该设置也常放在 MC.input 中(通过在 PASP.input 中“ %include MC.input ”使其生效)。该设置项可以在蒙特卡洛模拟(以及可能用到的共轭梯度下降优化)中添加外磁场,单位为T。例如在z方向提供0.1 T外磁场时,可以如案例1所示设置。
备注
在计算外磁场引起的能量变化( Zeeman 项)时,需要乘上磁性原子的磁矩值,而这个磁矩值是从“ block Spin_values ”中读取的。当且仅当“ block Spin_values ”设置的是真实的磁矩值(以为单位)时,所计算得到的 Zeeman 项才是正确的。但是前面提到,在假定自旋为1时,“ block Spin_values ”中磁性原子需要设置为2(而非真实磁矩值),这时可以有以下两种处理方式:
(1)参数值等各项设置不变,只按比例调整“ block ExternalMagneticField ”的设置值。当磁性原子的真实磁矩值为 \({\mu}\) (以 \({\mu}_B\) 为单位),真实自旋量子数大小为 \(S=\frac{1}{2} \mu\) (等式中只考虑数值,不考虑单位,下同),而“ block Spin_values ”中磁性原子设置为2时,“ block ExternalMagneticField ”的磁场单位实际为 \(\frac{2}{\mu} \mathrm{T}=\frac{1}{S} T\) 。换言之,当“ block ExternalMagneticField ”设置为0.1时,有效的磁场是 \(\frac{0.2}{\mu} \mathrm{T}=\frac{0.1}{S} T\) ;如需得到0.1 T的有效磁场,则需要将“ block ExternalMagneticField ”的相应分量取值设置为 \(0.1 S=0.05 \mu\) ,例如自旋量子数 \(S=\frac{3}{2}\) 时,应取值0.15,如案例2所示。
(2)按真实值设置“ block Spin_values ”和“ block ExternalMagneticField ”,这时需要按比例调整各参数值。自旋二次项的系数值需要除以 \(S^{2}\) ,自旋四次项的系数值需要除以 \(S^{4}\),以此类推。
案例1:
%block ExternalMagneticField 0 0 0.1 %endblock ExternalMagneticField
案例2(自旋矢量归一化模型,0.1T外磁场,自旋量子数为3/2情形):
%block Spin_values 0 0.15 0 %endblock Spin_values
参数名称:MD.B_x、MD.B_y、MD.B_z
默认值: 0.0
可选值: 实数
描述: MD的常用设置。分别用于设置在自旋动力学模拟过程中施加于体系的外磁场在x、y、z方向的分量,单位为T。
备注
由于MD中已使用该组设置项来设定外磁场,此时“
block ExternalMagneticField”的设置无效。由于MD对应的“
Model atomic_effective_H”中常取自旋归一化模型,即“block Spin_values”中磁性原子需要设置为2(磁矩大小为2 \({\mu}_B\) )。关于“block Spin_values”取值对有效磁场的影响,参见上一组设置项“block ExternalMagneticField”的相关说明。
案例:
MD.B_x 0.0d0 MD.B_y 0.0d0 MD.B_z 0.0d0
3.1.3 附属文件cell.str:晶胞信息¶
这个文件通常提供晶胞的信息(有时也可提供原胞或超胞信息)。如果在 PASP.input 中用到了“%block SuperCell”(参见3.1.2.2节),则会在 cell.str 提供的结构基础上进行扩胞。有时我们也可以直接在 cell.str 中提供超胞,而省去利用“ %block SuperCell ”扩胞的步骤。为了称谓的统一起见,在本软件的手册中,我们将总是称 cell.str 提供的结构为晶胞,经“%block SuperCell”扩胞的结构为超胞,而3.1.4节将介绍的 unit_cell.str 提供的结构为原胞。
使用 cell.str 作为输入文件时,须在 PASP.input 中添加行“%include cell.str”,否则 cell.str 文件无效。该文件的设置项也可以直接写在 PASP.input 文件中,并且在 PASP.input 文件中省略“%include cell.str”。
若在运行PASP软件的文件夹中无 cell.str 文件(无论在 PASP.input 中是否存在“%include cell.str”),在运行软件时会在相应文件夹下按照默认内容生成一个新的 cell.str 文件;但仅当 PASP.input 中存在“%include cell.str”时,按默认内容生成的 cell.str 文件内容才能被读取。
备注
注意:该文件中的部分设置项不可缺省。
默认的 cell.str 文件内容为:
NumberOfAtoms 1 number_of_species 1 LatticeConstant 1 Ang %block LatticeVectors 1 0 0 0 1 0 0 0 1 %endblock LatticeVectors %block AtomicCoordinatesAndAtomicSpecies 0 0 0 1 H 1 %endblock AtomicCoordinatesAndAtomicSpecies
以 \(BiTiO_{3}\) 为例, cell.str 文件可以写成:
#=========================================# NumberOfAtoms 5 number_of_species 3 LatticeConstant 1 Ang %block LatticeVectors 4.03331142642247 -0.0 -0.0 -0.0 4.03331142642247 -0.0 0.0 0.0 4.03331142642247 %endblock LatticeVectors AtomicCoordinatesFormat NotScaledCartesianAng %block AtomicCoordinatesAndAtomicSpecies 2.01665571 2.01665571 0.00000000 1 O 1 2.01665571 0.00000000 2.01665571 1 O 2 0.00000000 2.01665571 2.01665571 1 O 3 2.01665571 2.01665571 2.01665571 2 Ti 4 0.00000000 0.00000000 0.00000000 3 Ba 5 %endblock AtomicCoordinatesAndAtomicSpecies #=========================================#
以下3.1.3.1至3.1.3.6节将逐条解释各项设置的含义。软件也支持直接使用 POSCAR 文件代替或生成 cell.str 文件,相关设置方式见3.1.3.7节。3.1.3.8节将介绍如何利用已有的原胞结构文件(以 POSCAR 文件为例)扩胞得到相应的超胞的 POSCAR 和 cell.str 文件。
3.1.3.1 NumberOfAtoms¶
参数名称: NumberOfAtoms
默认值: 0
可选值: 非负整数
描述: 晶胞中原子数。
案例:
NumberOfAtoms 5
3.1.3.2 number_of_species¶
参数名称: number_of_species
默认值: 1
可选值: 非负整数
描述: 晶胞中元素种类数。
案例:
number_of_species 3
3.1.3.3 LatticeConstant¶
参数名称: LatticeConstant
默认值: 0.0 Bohr
可选值: 非负实数;Ang/Bohr
描述: 晶胞基矢的单位(由数值和单位构成),常用值为“1 Ang”,缺省值为“0.0 Bohr ”。“Ang”为埃(Å), “Bohr”为玻尔单位(1 Bohr约等于0.52917725埃)。
案例:
LatticeConstant 1 Ang
3.1.3.4 block LatticeVectors¶
参数名称: block LatticeVectors
默认值: 单位矩阵
可选值: 3×3可逆矩阵,矩阵元为实数
描述: 晶胞基矢信息。三行分别提供三个基矢的信息,每行的三个数据是基矢的三个笛卡尔坐标分量,以“LatticeConstant”(3.1.3.3节)的内容作为单位。
案例:
%block LatticeVectors 4.03331142642247 -0.0 -0.0 -0.0 4.03331142642247 -0.0 0.0 0.0 4.03331142642247 %endblock LatticeVectors
3.1.3.5 AtomicCoordinatesFormat¶
参数名称: AtomicCoordinatesFormat
默认值: NotScaledCartesianBohr
可选值: NotScaledCartesianAng/Ang/NotScaledCartesianBohr/Bohr/ScaledCartesian,ScaledByLatticeVectors/Fractional
描述: 晶胞中原子坐标的格式,常用值为“
NotScaledCartesianAng”,缺省值为“NotScaledCartesianBohr”。
有以下四种选项:
NotScaledCartesianBohr ”或“ Bohr ”,坐标按笛卡尔坐标输入,单位为Bohr;NotScaledCartesianAng ”或“ Ang ”,坐标按笛卡尔坐标输入,单位为埃;ScaledCartesian ”,坐标按笛卡尔坐标输入,单位为“LatticeConstant”的内容。ScaledByLatticeVectors ”或“ Fractional ”,坐标按分数坐标输入(具体地,用晶胞的三个基矢和坐标原点构造仿射坐标系,原子位置坐标用这个仿射坐标系下的坐标描述)。案例:
AtomicCoordinatesFormat NotScaledCartesianAng
3.1.3.6 block AtomicCoordinatesAndAtomicSpecies¶
参数名称: block AtomicCoordinatesAndAtomicSpecies
默认值: 不可缺省(缺省时报错”coo: You must specify the atomic coordinates”)。
可选值: 详见“描述”。
描述: 晶胞中原子坐标信息以及元素信息。每行对应原胞中的一个原子,前三个数据是三个坐标分量(格式由“AtomicCoordinatesFormat”内容指定),第四个数据为元素的编号(对于所研究体系中包含的元素,从1开始编号),第五个数据为元素的化学符号。软件只读取每行的前五个数据,后面的数据无效。习惯上,我们常在每行添加第六个数据,这个数据是原子的编号(对于所研究体系中的所有原子,从1开始编号)。
案例:
%block AtomicCoordinatesAndAtomicSpecies 2.01665571 2.01665571 0.00000000 1 O 1 2.01665571 0.00000000 2.01665571 1 O 2 0.00000000 2.01665571 2.01665571 1 O 3 2.01665571 2.01665571 2.01665571 2 Ti 4 0.00000000 0.00000000 0.00000000 3 Ba 5 %endblock AtomicCoordinatesAndAtomicSpecies
3.1.3.7 用POSCAR文件代替cell.str (READ_POSCAR)¶
参数名称: READ_POSCAR
默认值: F
可选值: T/F
描述: 如果已有晶胞的 POSCAR 文件(VASP软件的常用输入文件之一),也可以直接用它取代 cell.str 作为晶胞结构的输入文件。此时需要在 PASP.input 中将此项设为T;该项设置为T时,还会自动生成相应的 cell.str 文件。这里需要提供的 POSCAR 文件兼容以下两种格式:A.第一行提供任意内容,第五行提供各元素符号,第六行提供各元素的原子个数(参见3.1.3.8节格式A示例文件);B.第一行提供各元素符号,第五行直接提供各元素的原子个数(参见3.1.3.8节格式B示例文件)。
案例:
READ_POSCAR T
3.1.3.8 利用原胞的POSCAR文件扩胞¶
如果已有原胞 POSCAR 文件,想要生成相应的晶胞或超胞的 POSCAR 文件,可以利用脚本 post_VASP 实现。该脚本附在 “example_public/create_supercell” 文件夹下,使用前需要添加执行权限(例如“ chmod +x 路径/文件名 ”)。若还需获取对应晶胞或超胞的 cell.str 文件,可参见3.1.3.7节内容。
例如,假设已有 \(BiFeO_{3}\) 原胞(空间群R3c)的POSCAR(格式A):
#=========================================#
BiFeO3
1.00000000000000
5.7643603684609124 -0.0010632695629771 -0.0007349871303296
3.1487499916792472 4.8283770645635444 -0.0007349871303221
3.1487499916792459 1.7053535362982746 4.5171888309033719
Bi Fe O
2 2 6
Direct
0.2928365613303967 0.2928365613303967 0.2928365613303967
0.7928365613303967 0.7928365613303967 0.7928365613303967
0.0084017329201203 0.0084017329201203 0.0084017329201203
0.5084017299201236 0.5084017299201236 0.5084017299201236
0.6217457551533769 0.8807086125212393 0.2163073380748699
0.3807086125212393 0.1217457771533788 0.7163073230748722
0.8807086125212393 0.2163073380748699 0.6217457551533769
0.1217457771533788 0.7163073230748722 0.3807086125212393
0.2163073380748699 0.6217457551533769 0.8807086125212393
0.7163073230748722 0.3807086125212393 0.1217457771533788
#=========================================#
如需获得该POSCAR(原胞结构)所对应的超胞的 POSCAR 文件:首先需要删除第六行(在基矢信息和各元素原子数信息之间不要加元素名的行);第一行需要改成“Bi Fe O”,即提供各元素的化学符号。修改后POSCAR如下所示(格式B):
#=========================================#
Bi Fe O
1.00000000000000
5.7643603684609124 -0.0010632695629771 -0.0007349871303296
3.1487499916792472 4.8283770645635444 -0.0007349871303221
3.1487499916792459 1.7053535362982746 4.5171888309033719
2 2 6
Direct
0.2928365613303967 0.2928365613303967 0.2928365613303967
0.7928365613303967 0.7928365613303967 0.7928365613303967
0.0084017329201203 0.0084017329201203 0.0084017329201203
0.5084017299201236 0.5084017299201236 0.5084017299201236
0.6217457551533769 0.8807086125212393 0.2163073380748699
0.3807086125212393 0.1217457771533788 0.7163073230748722
0.8807086125212393 0.2163073380748699 0.6217457551533769
0.1217457771533788 0.7163073230748722 0.3807086125212393
0.2163073380748699 0.6217457551533769 0.8807086125212393
0.7163073230748722 0.3807086125212393 0.1217457771533788
#=========================================#
修改好POSCAR之后在相应文件夹下输入命令(Linux系统)“ 路径名/post_VASP ”(脚本在当前文件夹内时可用“ ./post_VASP ”),在显示出列表后输入“1”选择扩胞功能,再输入“1 1 1”选择1×1×1的扩胞(如需在这步生成超胞,则输入相应的扩胞比例即可,例如输入“2 2 2”选择2×2×2的扩胞),可在相应路径下生成 POSCAR.multi (扩胞后的POSCAR)、 POSCAR.multi.xyz (扩胞后各原子的笛卡尔坐标)和 xyz.dat (也是扩胞后各原子的笛卡尔坐标,格式略有不同)三个文件。其中 POSCAR.multi 重命名为POSCAR即可作为超胞的结构文件(可参照3.1.3.7节内容获得相应的 cell.str 文件)。
3.1.4 附属文件unit_cell.str:原胞信息¶
这个文件通常提供原胞的信息。为叙述方便起见,以下总是将 unit_cell.str 中定义的“胞”称为原胞。需要注意的是,unit cell这个术语的严格翻译是晶胞(也称单胞),但这里通常需要提供的是原胞(primitive cell)的信息。
使用 unit_cell.str 作为输入文件时,须在 PASP.input 中添加行“ %include unit_cell.str 否则 unit_cell.str 文件无效。该文件的设置项也可以直接写在 PASP.input 文件中,并且在 PASP.input 文件中省略“ %include cell.str ”。
若 unit_cell.str 文件缺失(且在 PASP.input 等输入文件中未提供相应的设置信息),则原胞信息将与 cell.str 所定义的晶胞信息一致。因此,当 cell.str 提供的是原胞信息时,可以省略 unit_cell.str 的设置信息(此时原胞与晶胞相同);否则一般不能省略 unit_cell.str 的相关设置内容(此时原胞与晶胞不同,需要另外定义原胞)。
通常, unit_cell.str 文件包含以下内容(以 \(BiTiO_{3}\) 为例):
#=========================================#
unit_cell.na 5
%block unit_cell_in_Ang
4.03331142642247 -0.0 -0.0
-0.0 4.03331142642247 -0.0
0.0 0.0 4.03331142642247
%endblock unit_cell_in_Ang
%block Atoms_in_unit_cell_Ang
2.01665571 2.01665571 0.00000000 1 O 1
2.01665571 0.00000000 2.01665571 1 O 2
0.00000000 2.01665571 2.01665571 1 O 3
2.01665571 2.01665571 2.01665571 2 Ti 4
0.00000000 0.00000000 0.00000000 3 Ba 5
%endblock Atoms_in_unit_cell_Ang
#=========================================#
以下3.1.4.1至3.1.4.3各节将逐条解释各项设置的含义。软件也支持直接使用 POSCAR_UC 文件代替或生成 unit_cell.str 文件,相关设置方式见3.1.4.4节。
3.1.4.1 unit_cell.na¶
参数名称: unit_cell.na
默认值: “
NumberOfAtoms”的取值(3.1.3.1节)。可选值: 非负整数
描述: 原胞中原子数。
案例:
unit_cell.na 5
3.1.4.2 block unit_cell_in_Ang¶
参数名称: block unit_cell_in_Ang
默认值: 缺省时原胞基矢与晶胞基矢相同(由“
block LatticeVectors”设置,参见3.1.3.4节)。可选值: 3×3可逆矩阵,矩阵元为实数
描述: 原胞基矢信息。三行分别提供三个基矢的信息,每行的三个数据是基矢的三个笛卡尔坐标分量,只能以埃作为单位。
案例:
%block unit_cell_in_Ang 4.03331142642247 -0.0 -0.0 -0.0 4.03331142642247 -0.0 0.0 0.0 4.03331142642247 %endblock unit_cell_in_Ang
3.1.4.3 block Atoms_in_unit_cell_Ang¶
参数名称: block Atoms_in_unit_cell_Ang
默认值: 缺省时该部分信息与晶胞一致(由“
block AtomicCoordinatesAndAtomicSpecies”设置,参见3.1.3.6节)。可选值: 略,详见“描述”
描述: 原胞中原子坐标信息以及元素信息。每行对应原胞中的一个原子,前三个数据是三个坐标分量(只能采用笛卡尔坐标,以埃为单位),第四个数据为元素的编号(对于所研究体系中包含的元素,从1开始编号),之后的数据不读取。为了与cell.str的相应内容保持格式一致,习惯上在每行后面补充两个数据——第五个数据为元素的化学符号,第六个数据为原子的编号(对于所研究体系中的所有原子,从1开始编号)。
备注
注意:
当软件用到 unit_cell.str 的相应内容时,由于软件只允许以埃为单位输入原胞的笛卡尔坐标信息,为了方便与统一起见,我们强烈建议在 cell.str 中也以埃为单位输入晶胞的笛卡尔坐标信息。即在 cell.str 中采用 “
LatticeConstant 1 Ang” 和“AtomicCoordinatesFormat NotScaledCartesianAng”两项设置。在 unit_cell.str 的原胞原子坐标部分也建议把每行的五个或六个数据写全(虽然软件只读取每行的前四个数据),使之与 cell.str 的晶胞原子坐标部分格式一致。在原胞与晶胞一致的简单情形下, unit_cell.str 的各项设置可以从 cell.str 的相应设置复制粘贴得到。在本软件中,晶胞和原胞必须采用同一套笛卡尔坐标系!换言之,晶胞任一基矢的信息(由坐标描述)必须是原胞三个基矢以整数为系数的线性组合。这里采用的笛卡尔坐标系通常是以晶胞的原点作为原点、以晶胞的a轴(第一个基矢)方向为x方向所建立的空间直角坐标系(右手系)。原胞的原点和晶胞的原点必须一致。特别注意,如果原胞的第一个基矢与晶胞a轴方向不一致,在描述原胞基矢和原胞内原子坐标时,千万不要利用原胞基矢重新建立一套新的笛卡尔坐标系。
案例:
%block Atoms_in_unit_cell_Ang 2.01665571 2.01665571 0.00000000 1 O 1 2.01665571 0.00000000 2.01665571 1 O 2 0.00000000 2.01665571 2.01665571 1 O 3 2.01665571 2.01665571 2.01665571 2 Ti 4 0.00000000 0.00000000 0.00000000 3 Ba 5 %endblock Atoms_in_unit_cell_Ang
3.1.4.4 用POSCAR_UC文件代替unit_cell.str (READ_POSCAR_UC)¶
参数名称: READ_POSCAR_UC
默认值: F
可选值: T/F
描述: 如果已有原胞的 POSCAR 文件(VASP软件的常用输入文件之一),也可以直接用它取代 unit_cell.str 作为原胞结构的输入文件。此时需要在 PASP.input 中将此项设为T;该项设置为T时,还会自动生成相应的 unit_cell.str 文件。这里需要提供的 POSCAR_UC 文件兼容以下两种格式:A.第一行提供任意内容,第五行提供各元素符号,第六行提供各元素的原子个数(参见3.1.3.8节格式A示例文件POSCAR);B.第一行提供各元素符号,第五行直接提供各元素的原子个数(参见3.1.3.8节格式B示例文件POSCAR)。
案例:
READ_POSCAR_UC T
3.1.5 附属文件MC.input:蒙特卡洛模拟与CG局域优化相关设置¶
使用 MC.input 作为输入文件时,须在 PASP.input 中添加行“ %MC.input ”,否则 MC.input 文件无效。该文件的设置项也可以直接写在 PASP.input 文件中,并且在 PASP.input 文件中省略“ %include MC.input ”。
MC.input 文件的相关设置在“
Model Spin_lattice_interaction”(2.1.3节)和“Model atomic_effective_H”(2.2.3节)中都会用到。前者主要用于较简单的磁性体系的蒙特卡洛模拟和CG(共轭梯度下降法)局域优化;后者功能类似,但适用范围更广(磁性、铁电、多铁等体系)。
3.1.5.1 自定义初态 (Read_init_spin)¶
参数名称: Read_init_spin
默认值: F
可选值: T/F
描述: 是否读取初始构型信息。若T,从相应文件中读取初始构型信息:“Model Spin_lattice_interaction”时读取 spin3.in 文件,“Model atomic_effective_H”时读取 amp_local_mode.in 文件。
案例:
Read_init_spin T
3.1.5.2 PTMC温度相关设置¶
参数名称: PT.M
默认值: 2
可选值: 正整数。必须是并行计算进程数的整数倍!
描述: 不同温度的副本个数。注意必须是并行计算进程数的整数倍,否则直接报错终止!
案例:
PT.M 64
参数名称: PT.low_temp
默认值: 0.1
可选值: 正实数
描述: 各温度副本中的最低温,Hartree单位,0.00001约等于3.15K。
案例:
PT.low_temp 0.000001
参数名称: PT.high_temp
默认值: 1.0
可选值: 正实数
描述: 各温度副本中的最高温,Hartree单位。
案例:
PT.high_temp 0.002
参数名称: PT.Tmesh
默认值: 1
可选值: 1/2
描述: 各温度副本的温度分布:1为反比(1/T均匀),2为正比(T均匀)。
案例:
PT.Tmesh 2
3.1.5.3 PTMC模拟步数与统计相关设置¶
PTMC的计算量与模拟步数近似成正比。决定PTMC步数的主要是 nblk 和 PT.nblk_T 两项设置(总计算时间近似与二者乘积成正比)。具体地,每轮MCS(蒙特卡洛模拟的一步)内,会依次尝试对每个自由度取值进行修改;nblk值是每两次温度副本交换步骤(交换步)之间有几轮MCS; PT.nblk_T 是一个大循环步骤中包含几个交换步,其中在 nbeg_nlk 个交换步之后的数据才会用于进行热力学统计(包括能量、热容等统计量),注意 nbeg_nlk 取值不能超过 PTMC的计算量与模拟步数近似成正比。决定PTMC步数的主要是 nblk 和 PT.nblk_T 两项设置(总计算时间近似与二者乘积成正比)。具体地,每轮MCS(蒙特卡洛模拟的一步)内,会依次尝试对每个自由度取值进行修改;nblk值是每两次温度副本交换步骤(交换步)之间有几轮MCS; PT.nblk_T 是一个大循环步骤中包含几个交换步,其中在 nbeg_nlk 个交换步之后的数据才会用于进行热力学统计(包括能量、热容等统计量),注意 nbeg_nlk 取值不能超过 PT.nblk_T ; PT.niter 是总共完成多少个大循环步骤(通常设为1)。
一般建议先将 PT.nblk_T 、 nbeg_blk 和 nblk 都取为较小的值,测试运行不出错后,再调成实际需要的设置值(可能需要按比例预估总计算时间,以防所需时间过长)。案例中提供的是比较推荐的设置值,但对应的计算量较大(对于复杂体系可能需要的计算时间较长);对于计算精度要求不太高或者在测试阶段,建议适当调小计算量( PT.nblk_T 、 nbeg_blk 和 nblk 三项设置大致等比例地减小即可)。
参数名称: nblk
默认值: 10
可选值: 非负整数。建议取10的整数倍。
描述: nblk值是每两次温度副本交换步骤(交换步)之间有几轮MCS(每轮MCS内,会依次尝试对每个自由度取值进行修改)。
案例:
nblk 500
参数名称: PT.nblk
默认值: 10
可选值: 非负整数。
描述:
PT.nblk_T是一个大循环步骤中包含几个交换步(温度副本交换步骤)。案例:
PT.nblk_T 4000
参数名称: PT.niter
默认值: 1
可选值: 非负整数。
描述:
PT.niter是总共完成多少个大循环步骤(每个大循环步骤中包含PT.nblk_T个交换步,其中在nbeg_nlk个交换步之后的数据用于进行热力学统计)。一般取1。案例:
PT.niter 1
参数名称: nbeg_blk
默认值: 0
可选值: 非负整数。
描述: 在一个大循环步骤中,
nbeg_nlk个交换步之后的数据用于进行热力学统计(包括能量、热容等统计量),注意nbeg_nlk取值不能超过PT.nblk_T。案例:
nbeg_blk 2000
参数名称: PT.ninterval
默认值: 10
可选值: 正整数。
描述: 在进行热力学统计阶段,每完成
PT.ninterval轮MCS步骤统计一次数据。案例:
PT.ninterval 1
参数名称: PT.nmeasure
默认值: 0
可选值: 非负整数。
描述: 完成PTMC后,再补充进行
PT.nmeasure轮MCS步骤(不涉及温度副本交换),用于计算统计量。通常设为0。案例:
PT.nmeasure 0
3.1.5.4 MC相关的其他设置¶
参数名称: MC
默认值: F
可选值: T/F
描述: 是否开启MC功能(本功能与MD功能不可同时开启,参见3.1.6节)。MC表示蒙特卡洛模拟。
案例:
MC T
参数名称: Parallel_Tempering
默认值: F
可选值: T/F
描述: 在已开启MC功能的前提下,是否开启PTMC功能。PTMC表示并行退火蒙特卡洛模拟,该方法中需用到多个不同温度的副本。
案例:
Parallel_Tempering T
参数名称: atom_Heff.homogeneous_strain
默认值: T
可选值: T/F
描述: 是否开启整体的(均匀)应变自由度。
案例:
atom_Heff.homogeneous_strain F
参数名称: atom_Heff.inhomogeneous_strain
默认值: F
可选值: T/F
描述: 是否开启局域的(非均匀)应变自由度。
案例:
atom_Heff.inhomogeneous_strain F
参数名称: Temperature
默认值: 0.0
可选值: 非负实数
描述: MC中的温度,Hartree单位。在使用PTMC功能时,本设置项不起作用,温度由3.1.5.2节相应设置决定。
案例:
Temperature 0.1
参数名称: global.heat_bath
默认值: F
可选值: T/F
描述: 是否采用heat bath方法,T表示选用heat bath方法,F表示采用默认的Metropolis方法。处理磁性体系时heat bath算法更为高效 18 ;但该算法的使用条件较为局限,所以即使设置为T,也是只有符合适用条件时才会采用这个较高效的算法,而不符合条件时仍采用默认方法。该算法目前仅在“
Model Spin_lattice_interaction”中支持使用,而在更具通用性的“Model atomic_effective_H”中无法使用。案例:
global.heat_bath T
参数名称: atom_Heff.auto_adjust_try_amp
默认值: T
可选值: T/F
描述: “Model atomic_effective_H”中每次随机修改局域模式或应变模式值时,最大程度的修改量,是否自动随时调整。通常取T,不建议修改。
案例:
atom_Heff.auto_adjust_try_amp T
参数名称: atom_Heff.try_amp.change_rate
默认值: 1.5
可选值: T/F
描述: “Model atomic_effective_H”中“
atom_Heff.auto_adjust_try_amp”取T时,每次随机修改局域模式或应变模式值时,最大程度的修改量可自动随时调整,每次自动调整时乘或除以该设置值。不建议修改。案例:
atom_Heff.try_amp.change_rate 1.5
参数名称: spin_lat.general_J
默认值: F
可选值: T/F
描述: 在“Model Spin_lattice_interaction”中,是否以矩阵形式提供J矩阵等参数。主要影响到输入文件 spin_exchange.dat 的格式。取T时,每对原子间的相互作用参数需要提供9个数(矩阵信息);取F时,每对原子间的相互作用参数仅需提供1个数(即各向同性的J值)。参见3.3节。
案例:
spin_lat.general_J T
参数名称: spin_lat.LJmatSym
默认值: F
可选值: T/F
描述: 在“Model Spin_lattice_interaction”中,以矩阵形式提供J矩阵等参数时(即“
spin_lat.general_J”取T时),是否根据所涉及的原子所满足的空间对称性的要求,将描述两体相互作用的J矩阵(或描述单体项的SIA矩阵)修正成符合对称性的形式。通常在“spin_lat.general_J”取T时也应取T。案例:
spin_lat.LJmatSym T
参数名称: spin_lat.Ising
默认值: F
可选值: T/F
描述: 在“Model Spin_lattice_interaction”中,是否采用Ising模型(即自旋仅上下两种取值)。
案例:
spin_lat.Ising F
3.1.5.5 CG局域优化的相关设置¶
参数名称: atom_Heff.relax_str
默认值: F
可选值: T/F
描述: 在“Model atomic_effective_H”中是否开启CG局域优化。
案例:
atom_Heff.relax_str T
参数名称: spin_lat.relax_str
默认值: F
可选值: T/F
描述: 在“Model Spin_lattice_interaction”中是否开启CG局域优化。
案例:
spin_lat.relax_str T
参数名称: opt.NSW
默认值: 100
可选值: 非负整数
描述: CG局域优化的最大步数。每一步CG需要相应地完成一次对尝试构型的能量估计(使用相应的有效哈密顿量模型)。
案例:
opt.NSW 1000
参数名称: opt.EDIFFG
默认值: 1.0E-5
可选值: 正或负实数
描述: CG精度设置,达到精度时自动结束CG优化。设置值为正时用相邻两步CG优化(对应两个不同优化方向)的能量变化小于设置值作为达到精度的条件,为负时要求所有自由度受力均小于设置值时作为达到精度的条件。
案例:
opt.EDIFFG -0.1E-06
3.1.5.6 MC和CG中添加约束条件¶
参数名称: block local_mode.MC_mode_range
默认值: 不限制取值范围
可选值: 实数
描述: 在使用“Model atomic_effective_H”的MC或CG功能时,可能用到该设置。这里可以设置在MC或CG过程中各个局域模式和应变的取值范围(硬边界),共需“局域模式数+6”行:其中局域模式数应与测试运行时名为local_mode-*.xsf(*处为编号)的输出文件的个数一致,而这个个数未必与“block local_mode.mode_definition”部分定义的局域模式数一致(因为PASP软件可能会根据对称性分析补充对称等价的局域模式);“+6”部分对应应变的六个自由度。每行设置两个值,依次是最大值和最小值,用于限定各个模式的“
硬边界”。这里所谓硬边界是指模式值超出边界值时会被强行拉回到边界值。相应地,若采用能量指数上升等方法限制取值范围的方式,我们称之为“软边界”,局域模式的“软边界”设置参见3.1.7.5节类型二的相关内容,应变模式的“软边界”设置将在下一条设置项提及。若希望完全固定某个模式的取值,只需要将“硬边界”的最大值和最小值设置成相等,例如案例中的最后两个模式。案例:
%block local_mode.MC_mode_range #取值范围:最大值,最小值(硬边界) 0.3 -0.3 -0.3 -0.5 0.4 0.3 0.1 0.1 0.1 0 0 -0.1 0.4 0.0 0 0.0 0.2 0.2 %endblock local_mode.MC_mode_range
参数名称: block local_mode.lamp_strain
默认值: 不限制取值范围,左边界缺省时取右边界的相反数
可选值: 右边界为正实数,左边界为负实数
描述: 在使用“Model atomic_effective_H”的MC或CG功能时,可能用到该设置。这里可以设置在MC或CG过程中,各个应变模式的“软边界”(参见3.1.7.5节类型二“lamp”的相关内容,在那里可以设置各个局域声子模式的“软边界”)。这里软边界形式总是采用3.1.7.5节类型二中提到的形式二,即 \(A+Bu+\text{coef}*e^{\text{scale}*\left(u/u_{c}-1\right)}\) 。其中, \(u\) 表示应变的幅度; \(u_{c}\) 为截断幅度,当 \(u>0\) 时取 \(u_{c2}\) ,当 \(u<0\) 时取 \(u_{c1}\) ; \(scale\) (大于0)为输入文件中用“
local_mode.non_polynomial.exp.scale”设置的值(缺省值为6.0); \(coef\) (大于0)是输入文件中用“local_mode.non_polynomial.exp.coefficient”设置的值(缺省值为1.0);根据边界 \(u=u_{c1}<0\) 和 \(u=u_{c2}>0\) 处能量(考虑应变的单体能量贡献即可)及其导数连续的条件可以分别在两个边界处解出各自的 \(A\) 和 \(B\) , \(u>0\) 时采用 \(u=u_{c2}\) 处解出的 \(A\) 和 \(B\) ,而 \(u<0\) 时采用 \(u=u_{c1}\) 处解出的 \(A\) 和 \(B\) 。共需6行内容,依次对应应变的六个自由度。每行内容需要先写右边界 \(u_{c2}\) (大于零),后写左边界 \(u_{c1}\) (小于零);左边界缺省时取右边界的相反数。案例:
%block local_mode.lamp_strain #strain取值范围:右边界>0(,左边界<0) 0.1 -0.1 0.2 -0.1 0.1 -0.1 0.3 -0.4 0.1 -0.1 0.1 -0.1 %endblock local_mode.lamp_strain
参数名称: local_mode.non_polynomial.exp.scale
默认值: 6.0
可选值: 正实数
描述: 在使用“Model atomic_effective_H”的MC或CG功能时,可能用到该设置。用于设置在MC或CG过程中,“软边界”(参见3.1.7.5节类型二“lamp”的相关内容)中的
scale参数。案例:
local_mode.non_polynomial.exp.scale 6.0
参数名称: local_mode.non_polynomial.exp.coefficient
默认值: 1.0
可选值: 正实数
描述: 在使用“Model atomic_effective_H”的MC或CG功能时,可能用到该设置。用于设置在MC或CG过程中,“软边界”(参见3.1.7.5节类型二“lamp”的相关内容)中的
coef参数。案例:
local_mode.non_polynomial.exp.coefficient 1.0
参数名称: block local_mode.set_strain_equal
默认值: F
可选值: T/F
描述: 在使用“Model atomic_effective_H”的MC或CG功能时,或者“Model Invariant”的随机生成构型功能时,可能用到该设置。这里可以设置某些应变模式的取值保持相等。用 \(\eta_{i}(i=1,2, \ldots, 6)\) 表示6种局域模式,则该block的六个数据(T或F)依次表示是否保持 \(\eta_{1}=\eta_{2}, \eta_{1}=\eta_{3}, \eta_{2}=\eta_{3}, \eta_{4}=\eta_{5}, \eta_{4}=\eta_{6}\text{和}\eta_{5}=\eta_{6}\) 。例如案例的设置会自动保持 \(\eta_{2}=\eta_{3}\text {和}\eta_{4}=\eta_{5}=\eta_{6}\) 。注意如果需要保持相等的若干模式所受的力不同,或受到的约束条件不一致(例如硬边界不一致),总是以编号小的模式的受力和取值为准。
案例:
%block local_mode.set_strain_equal F F T T F T %endblock local_mode.set_strain_equal
3.1.6 附属文件MD.input:分子动力学模拟相关设置¶
使用 MD.input 作为输入文件时,须在 PASP.input 中添加行“%MD.input”,否则 MD.input 文件无效。该文件的设置项也可以直接写在 PASP.input 文件中,并且在 PASP.input 文件中省略“%include MD.input”。
目前PASP仅在“Model atomic_effective_H”情形下支持MD模拟功能,参见2.2.4节介绍。这里补充介绍一些在 MD.input 中独有的设置项。
参数名称: atom_Heff.MD
默认值: F
可选值: T/F
描述: 是否开启MD模拟功能(本功能与MD功能不可同时开启,参见3.1.5.4节)。MD表示分子动力学模拟。
案例:
atom_Heff.MD T
参数名称: block atom_Heff.MASS_local_mode
默认值: 缺省时全部赋值为1.0
可选值: 正实数
描述: MD的常用设置。提供各局域模式的等效相对原子质量信息。提供的的质量数目即为局域模式的总数目(不计入应变模式,这与“Model Invariant”阶段产生的 local_mode-*.xsf 文件个数一致),顺序通常按照“block local_mode.mode_definition”中定义各局域模式时确定的先后顺序(如果实际局域模式数大于定义中写出的局域模式数,这时顺序应当与 local_mode-*.xsf 文件的编号一致)。局域模式仅涉及一个原子时,取元素的相对原子质量;涉及多个原子时,则需要使用相应的有效质量(例如局域声子模式,常以模式定义中各原子位移的平方为权重取相对原子质量的加权平均值)。
案例:
%block atom_Heff.MASS_local_mode 54.938 54.938 54.938 ……(省略中间部分数据) 15.999 15.999 15.999 %endblock atom_Heff.MASS_local_mode
参数名称: MD.Delta_t
默认值: 1.0
可选值: 正实数
描述: MD的常用设置。用于设置动力学模拟的单步时长,单位为飞秒(fs),一般设置在0.1-1.0范围内。若步长过小,则会使得模拟所需的计算时间过长;若步长过大,则会使得模拟效果失真,例如在NVE模拟中,系统的总能量将无法很好地保持恒定。
案例:
MD.Delta_t 0.5
参数名称: atom_Heff.MD_time
默认值: 10 * MD.Delta_t
可选值: 正实数
描述: MD的常用设置。用于设置动力学模拟的总时长,单位为飞秒(fs),软件运行所需时间基本上与动力学模拟的总步数(总时长除以单步时长)成正比。
案例:
atom_Heff.MD_time 4.0d3
参数名称: SLD.mode
默认值: 3
可选值: 1/2/3
描述: MD的常用设置。用于设置动力学模拟的模式,1表示仅考虑原子位移自由度的传统分子动力学模拟,2表示仅考虑自旋方向自由度的原子自旋动力学模拟,3表示同时考虑两类自由度的自旋晶格动力学模拟,目前MD模拟部分尚不支持模拟除位移自由度和自旋自由度以外的其他自由度。
案例:
SLD.mode 2
参数名称: LLG.method
默认值: 1
可选值: 1/2/3
描述: MD的常用设置。用于选择积分LLG方程(参见2.2.4节)时采用的数值算法,1表示4th-order Runge-Kutta method,2表示Mentink’s SIB method,3表示McLachlan’s SMP method。其中,方法1尚不支持NVT模拟,方法3原则上保证积分过程能量守恒,尚不支持并行计算,因而目前最常用的是方法2。
案例:
LLG.method 2
参数名称: LLG.damping
默认值: 0.0
可选值: 非负实数
描述: MD的常用设置。用于设置LLG方程(参见2.2.4节)的阻尼系数。该值非零时,程序将基于设定的“
MD.temperature”参数做NVT模拟;当该值为零时,软件将执行NVE模拟。案例:
LLG.damping 1.0d-2
参数名称: MD.damping
默认值: 0.0
可选值: 非负实数
描述: MD的常用设置。用于设置Newton方程(参见2.2.4节)的阻尼系数。该值非零时,程序将基于设定的“
MD.temperature”参数做NVT模拟,当该值为零时,程序将执行NVE模拟。目前,PASP软件尚不支持除NVT和NVE之外的其他系综模拟。案例:
MD.damping 4.0d-2
参数名称: MD.temperature
默认值: 0.0
可选值: 非负实数
描述: MD的常用设置。用于设置在NVT模拟时希望体系达到并保持的热平衡温度,单位为开尔文(K)。此外,该温度也将用于计算体系的热容和磁化率。
案例:
MD.temperature 300.0
参数名称: MD.aft_step
默认值: 1
可选值: 非负整数
描述: MD的常用设置。用于设置在经历初始多少步的模拟之后开始对体系做测量,目前程序仅支持对体系的温度、能量、热容、平均磁化强度、磁化率等统计量做相应的测量计算。
案例:
MD.aft_step 1
参数名称: MD.int_step
默认值: 1
可选值: 正整数
描述: MD的常用设置。用于设置相邻两次统计测量之间的间隔步数。
案例:
MD.int_step 10
参数名称: MD.init_velocity_temp
默认值: 0.0
可选值: 非负实数
描述: MD的常用设置。以温度作为表征,单位为开尔文(K),根据麦克斯韦速度分布律,设置体系初始的原子速度分布。
案例:
MD.init_velocity_temp 0.0d0
参数名称: MD.output_amp_lm
默认值: F
可选值: T/F
描述: MD的常用设置。用于设置是否输出MD模拟过程中的体系构型(包括原子位移和自旋方向),两次相邻输出之间的时间间隔由
MD.int_step参数决定。案例:
MD.output_amp_lm F
3.1.7 有效哈密顿量方法常用设置项¶
这里主要介绍使用“ Model Invariant ”构造有效哈密顿量阶段的常用设置项,其中多数设置项在后续的MC或MD模拟(“Model atomic_effective_H”)中也常继续使用;此外在“ Model find_J_path_sym ”(找不等价作用对)中需要用到的常用设置项也会在本节介绍。通常在MC或MD中需要额外补充的设置建议另外放在附属文件 MC.input 或 MD.input 中,并在 PASP.input 中添加行“%include MC.input”或“%include MD.input”使之生效。 MC.input 和 MD.input 的常用相关设置项见3.1.5节和3.1.6节。
3.1.7.1 展开体数 (fig.maxk)¶
参数名称: fig.maxk
默认值: 2
可选值: 非负整数
描述: 在有效哈密顿量方法模块中常用,在“
Model find_J_path_sym”(找不等价作用对)中也会用到。在这里设定最多考虑到几体相互作用,缺省值为2。案例为考虑到四体。案例:
fig.maxk 4
3.1.7.2 截断距离 (block fig.mdist)¶
参数名称: block fig.mdist
默认值: 不可缺省!(缺省时报错“read_fig_data: no fig.mdist block”)
可选值: 第一位取1,之后各位为正实数
描述: 在有效哈密顿量方法模块中常用,在“Model find_J_path_sym”(找不等价作用对)中也会用到。在这里设定相互作用的截断距离,注意单位是Bohr。第一位填1,第二位填两体相互作用的截断距离,第三位填三体相互作用的截断距离(其中任意两个原子的距离都不超过截断距离),以此类推。例如,只考虑到两体相互作用,截断距离为15 Bohr时,只需要填两个数据,如案例所示。
案例:
%block fig.mdist 1 15 %endblock fig.mdist
3.1.7.3 展开阶数相关设置¶
本节提及的各设置项主要用于在有效哈密顿量方法的“Model Invariant”
参数名称: GSM.maxpower
默认值: 通常缺省值为1;少数情形读取“
fitting.maxpower”的设置值作为缺省值,而“fitting.maxpower”的缺省值为2。这里少数情形仅包括“Model Fitting”和“Model Cluster_expansion”(使用蒙特卡洛模拟功能时),这两种Model在本手册中均未涉及。鉴于不同Model情形下该项设置的缺省值不同,当需要用到该项设置时,强烈建议明确地写出设置值而不要缺省。可选值: 非负整数
描述: 在有效哈密顿量方法模块中,使用点乘形式的磁相互作用时,常用该设置。本设置项用于设置点乘形式相互作用的最大展开阶数,但须注意最大展开阶数是GSM.maxpower的二倍。例如,展开到四阶点乘项时,可取值为2,如案例所示。
案例:
GSM.maxpower 2
参数名称: Invariant.power
默认值: 4
可选值: 非负整数
描述: 在有效哈密顿量方法模块中常用。在这里设置所有形式相互作用的最大展开阶数,缺省值为4。
案例:
Invariant.power 4
参数名称: Invariant.strain_power
默认值: 1
可选值: 非负整数
描述: 在有效哈密顿量方法模块中常用。在这里设置在应变与局域模式的交叉项中应变贡献部分的最大阶数,缺省值为1。例如,不考虑应变与局域模式交叉项时,可设置为0。
案例:
Invariant.strain_power 0
参数名称: Invariant.pure_strain_power
默认值: 2
可选值: 非负整数
描述: 在有效哈密顿量方法模块中常用。在这里设置纯应变项的最大展开阶数,缺省值为2。例如,纯应变项展开到四阶项时,可如案例所示设置。
案例:
Invariant.pure_strain_power 4
参数名称: block local_mode.power
默认值: 由前述各设置项决定各种相互作用的阶数
可选值: 非负整数
描述: 在有效哈密顿量方法模块中可能用到该设置项。在此可以更具体地设置指定类型相互作用的最大展开阶数,本设置项的优先级高于前述的各个设置项,但本设置项未明确指出的相互作用类型的展开阶数仍由前述各设置项决定。在“block local_mode.power”中可以有两部分内容:第一部分设置不同体数的相互作用的最大展开阶数;第二部分可以设置具体到第几种几体相互作用的最大展开阶数。在以下各案例中,我们均假定已设置“
Invariant.power 2”和“fig.maxk 2”(默认考虑到二阶,最多考虑两体)。案例1仅设置第一部分内容,即设置不同体数的相互作用的最大展开阶数;这里单体保留到6阶,二体仍保留到2阶。案例2仅设置第二部分内容,即设置不同体数的相互作用的最大展开阶数;这里设置第一类单体保留到6阶,前两类两体相互作用(一般是最近邻和次近邻)保留到4阶,而其他相互作用仍保留到2阶。案例3同时设置两部分内容;这里设置所有的单体保留到6阶,前三类(一般是前三近邻)的两体相互作用保留到4阶,而其他相互作用仍保留到2阶。
备注
注意:当单体相互作用的阶数大于6,或者二体(及以上)相互作用的阶数大于4时,软件常常慢的离谱。因此以目前PASP软件的优化程度,建议限制在上述阶数范围以内。
案例1:
%block local_mode.power 1 #以下需读取多少行设置(1行) 1 6 #1体 保留到6阶 %endblock local_mode.power
案例2:
%block local_mode.power 0 #第一部分:以下需读取多少行设置(0行,因为这里不设置第一部分) 3 #第二部分:以下需读取多少行设置(3行) 1 1 6 #1体 第1种 保留到6阶 2 1 4 #2体 第1种 保留到4阶 2 2 4 #2体 第2种 保留到4阶 %endblock local_mode.power
案例3:
%block local_mode.power 1 #第一部分:以下需读取多少行设置(1行) 1 6 #1体 保留到6阶 3 #第二部分:以下需读取多少行设置(5行) 2 1 4 #2体 第1种 保留到4阶 2 2 4 #2体 第2种 保留到4阶 2 3 4 #2体 第3种 保留到4阶 %endblock local_mode.power
3.1.7.4 SOC相关设置¶
参数名称: Invariant.SOC
默认值: T
可选值: T/F
描述: 在有效哈密顿量方法模块中,处理磁性体系时常用。用于设定是否考虑SOC(自旋轨道耦合)。
案例:
Invariant.SOC T
参数名称: local_mode.GSM2lm_int
默认值: F
可选值: T/F
描述: 在有效哈密顿量方法模块中,处理磁性体系时常用。用于设定在不考虑SOC(自旋轨道耦合)的前提下(即“Invariant.SOC F”时),各项是否统一采用自旋点乘(或若干组点乘的乘积)的形式。本项取T时,需搭配使用“
GSM.maxpower”设置项来设定展开阶数(参见3.1.7.3节)。案例:
local_mode.GSM2lm_int T
参数名称: block local_mode.special_SOC
默认值: 由“Invariant.SOC”决定
可选值: 非负整数
描述: 在有效哈密顿量方法模块中,处理磁性体系时可能用到该设置。用于更具体地指定哪些相互作用考虑SOC,哪些不考虑。第一行数据用于指定后面读取多少行信息。后面每行信息有三个数据,分别是几体、相应“几体”的第几种原子对(或原子簇)、该原子对(或原子簇)考虑SOC的相互作用最多保留到几阶(非SOC形式仍可以考虑到更高阶,这由3.1.7.3节各项设置决定)。比如案例中,实际上枚举了截断体数和截断距离内的所有的原子对和原子簇情形。并设置成仅单体项考虑SOC,保留到四阶;其余相互作用项均不考虑SOC。如果希望将最近邻的两体相互作用项保留二阶的SOC相互作用,则将“2 1 0”改成“2 1 2”即可。如果一开始不确定每种体数涉及几种原子对或原子簇,可以先缺省该项设置运行一遍,在输出文件 all_interaction_type_Spin_xyzform.dat 或 local_mode_PM.dat 文件中查得相应信息(参考2.2.1.1节对这两种输出文件的介绍)。
案例:
%block local_mode.special_SOC 11 1 1 4 2 1 0 2 2 0 2 3 0 2 4 0 2 5 0 3 1 0 3 2 0 3 3 0 3 4 0 4 1 0 %endblock local_mode.special_SOC
3.1.7.5 自定义局域模式 (block local_mode.mode_definition)¶
参数名称: block local_mode.mode_definition
默认值: 需要用到该数据时,通常不可缺省。
可选值: 非负整数
描述: 在有效哈密顿量方法模块中常用。在这里定义局域模式,这里的局域模式可以是自旋模式,也可以是局域声子模式等。以下分类型提供示例。
类型一: 自旋模式。以 \(TbMnO_{3}\) 为例,一个原胞中包含4个Mn原子,需要为原胞中的所有Mn原子(必须提供笛卡尔坐标)分别设置三个方向的自由度,如案例1所示。
案例1:
%block local_mode.mode_definition 2 # method, 2 is the general one, as below(填2,不需要改) 12 # num of modes(总模式数) 1 spin #该模式涉及1个原子,为自旋模式 2 #原子的元素编号(block Z_value排序) 2.646572590 0.000000000 0.000000000 1.0 0.0 0.0 #笛卡尔坐标;自旋方向x #两种模式之间必须空一行(软件需要读取一个空行) 1 spin 2 2.646572590 0.000000000 0.000000000 0.0 1.0 0.0 #笛卡尔坐标;自旋方向y 1 spin 2 2.646572590 0.000000000 0.000000000 0.0 0.0 1.0 #笛卡尔坐标;自旋方向z 1 spin 2 0.000000000 2.919204950 0.000000000 1.0 0.0 0.0 1 spin 2 0.000000000 2.919204950 0.000000000 0.0 1.0 0.0 1 spin 2 0.000000000 2.919204950 0.000000000 0.0 0.0 1.0 1 spin 2 2.646572590 0.000000000 3.701255083 1.0 0.0 0.0 1 spin 2 2.646572590 0.000000000 3.701255083 0.0 1.0 0.0 1 spin 2 2.646572590 0.000000000 3.701255083 0.0 0.0 1.0 1 spin 2 0.000000000 2.919204950 3.701255083 1.0 0.0 0.0 1 spin 2 0.000000000 2.919204950 3.701255083 0.0 1.0 0.0 1 spin 2 0.000000000 2.919204950 3.701255083 0.0 0.0 1.0 #最后可以继续空一行,也可以不空这行。 %endblock local_mode.mode_definition
备注
为了输出文件更具可读性,建议按x、y、z的顺序依次提供每个磁性原子的自旋自由度。
虽然在具有高对称性的体系中,可能仅提供x方向的自旋自由度,软件就能自动补充分析出y和z方向的自由度;但是在对称性较低的情形下,是不能自动补充分析出y和z方向自由度的。因此,为了统一起见,建议总是写全x、y、z方向的自由度。
类型二: 局域声子模式。以 \(BaTiO_{3}\) 为例,原胞中包含一个Ti原子,我们可以以Ti原子为中心定义局域声子模式(包含Ti及其周围原子共15个原子),如案例2所示。
案例2:
%block local_mode.mode_definition 2 # method, 2 is the general one, as below(填2,不需要改) 1 # num of modes(总模式数) 15 #该模式涉及15个原子,默认为局域声子模式(需读取15行坐标及位移) 2 1 1 1 1 1 1 3 3 3 3 3 3 3 3 #依次列出各原子的元素编号(block Z_value排序) 2.01665571 2.01665571 2.01665571 0.0 0.0 0.84914560 #Ti 坐标&位移,下同 2.01665571 0.00000000 2.01665571 0.0 0.0 -0.12643559 #O1 4.03331143 2.01665571 2.01665571 0.0 0.0 -0.12643559 #O1 2.01665571 4.03331143 2.01665571 0.0 0.0 -0.12643559 #O1 0.00000000 2.01665571 2.01665571 0.0 0.0 -0.12643559 #O1 2.01665571 2.01665571 0.00000000 0.0 0.0 -0.31944756 #O2 2.01665571 2.01665571 4.03331143 0.0 0.0 -0.31944756 #O2 0.00000000 0.00000000 0.00000000 0.0 0.0 0.03693648 #Ba 4.03331143 0.00000000 0.00000000 0.0 0.0 0.03693648 #Ba 4.03331143 4.03331143 0.00000000 0.0 0.0 0.03693648 #Ba 0.00000000 4.03331143 0.00000000 0.0 0.0 0.03693648 #Ba 0.00000000 0.00000000 4.03331143 0.0 0.0 0.03693648 #Ba 4.03331143 0.00000000 4.03331143 0.0 0.0 0.03693648 #Ba 4.03331143 4.03331143 4.03331143 0.0 0.0 0.03693648 #Ba 0.00000000 4.03331143 4.03331143 0.0 0.0 0.03693648 #Ba %endblock local_mode.mode_definition
备注
各原子的位移值只有相对大小是重要的,不需要关心单位。因为软件内部会对模式所包含的所有位移值的整体作归一化处理(归一化后各位移值的平方和为1 Bohr2)。后续在描述这个局域模式的大小时,例如0.5表示该模式涉及的所有原子都按上述归一化处理后的位移值乘0.5移动。
在案例2中,第四行(有效内容为“15”)有时需要改写成“15 lamp 其他数据”的形式,其中lamp含义为large amplitude,用于设置该模式幅度过大时的处理方式。具体的处理方式是,当某模式取值超出合理的范围 \(G\) 时,采用能量随模式幅度的绝对值指数上升的形式(代替原来的多项式形式),以避免因模型外推效果不佳而误认为模式幅度趋于无穷大时能量趋于负无穷。我们习惯上称 \(u=u_{c1}\) 和 \(u=u_{c2}\) 为软边界,因为实际上并没有严格地将模式取值限制在边界之内;相反,若希望严格限制模式的取值范围,可以参见3.1.5.6节内容。模式取值超出软边界时,对于该模式的单体项对能量的贡献,我们支持采用以下两种函数形式:形式一, \(G\) ;形式二, \(G\) 。其中, \(u\) 表示局域模式的幅度; \(u_{c}\) 为截断幅度,当 \(u>0\) 时取 \(u_{c2}\) ,当 \(u<0\) 时取 \(u_{c1}\) ; \(scale\) (大于0)为输入文件中用“
local_mode.non_polynomial.exp.scale”设置的值(缺省值为6.0); \(coef\) (大于0)是输入文件中用“local_mode.non_polynomial.exp.coefficient”设置的值(缺省值为1.0);根据边界 \(u=u_{c1}\) 和 \(u=u_{c2}\) 处能量(考虑单体能量贡献即可)及其导数连续的条件可以分别在两个边界处解出各自的 \(A\) 和 \(B\) , \(u>0\) 时采用 \(u=u_{c2}\) 处解出的 \(A\) 和 \(B\) ,而 \(u<0\) 时采用 \(u=u_{c1}\) 处解出的 \(A\) 和 \(B\) 。需要注意的是,形式一中不能保证解出的 \(B>0\) ,遇到 \(B≤0\) 情形时,软件无法正常运行;而形式二总能保证指数函数项的系数为正,因此稳定性较高。此外还需要注意,由于是采用指数函数形式控制幅度,蒙特卡洛模拟给出的基态结果仍然可能出现某些局域模式幅度的绝对值超出了“截断幅度”的情形,此时基态结果并不可靠(因为幅度超出截断值后的能量值是“非物理的”),出现这种情况的原因一般是模型不够准确或者截断距离的设置值不合适。
类型三: 多种模式混合定义。格式与上述各类型一致,只是在定义各个模式时可以采用不同类型的定义。如案例3中混合定义了磁性原子的自旋模式和所有原子的位移模式。需要再次强调的是,不同模式的定义之间必须空一行!
案例3:
%block local_mode.mode_definition 2 # method, 2 is the general one, as below 60 # num of modes 1 spin 1 4.246239888184 4.246239888184 4.246239888184 1.0 0.0 0.0 1 spin 1 4.246239888184 4.246239888184 4.246239888184 0.0 1.0 0.0 1 spin 1 4.246239888184 4.246239888184 4.246239888184 0.0 0.0 1.0 ……(为节省篇幅,省略中间部分内容) 1 3 5.215531205855 5.215531205855 7.523188458697 1.0 0.0 0.0 1 3 5.215531205855 5.215531205855 7.523188458697 0.0 1.0 0.0 1 3 5.215531205855 5.215531205855 7.523188458697 0.0 0.0 1.0 %endblock local_mode.mode_definition
3.1.7.6 读取已有相互作用信息 (local_mode.read_interaction)¶
参数名称: local_mode.read_interaction
默认值: F
可选值: T/F
描述: 在有效哈密顿量方法模块中常用(包括后续的MC或MD模拟等)。在这里设置是否直接从 local_mode_PM.dat 文件中读取相互作用信息。这里用到的 local_mode_PM.dat 文件本来是分析不等价相互作用时的输出文件,如果需要再次在相同的原胞结构(参见3.1.4节)、局域模式定义、体数、截断距离、展开阶数、SOC的保留阶数等设置下调用PASP,例如获取不同构型的 *.ene_symbol 文件(允许处理不同的超胞)时,或进行后续的MC和MD模拟时,就可以直接从已有的该文件中读取所需信息。特别是使用MC或MD功能时,因为通常需要并行计算,而使用“
Model Invariant”获取 local_mode_PM.dat 文件的步骤暂不支持并行,因此在MC或MD阶段常常必须设置该项为T,以便直接读取 local_mode_PM.dat 文件内容。案例:
local_mode.read_interaction T
3.1.7.7 随机生成构型或自定义构型的相关设置¶
参数名称: Invariant.cal_para
默认值: F
可选值: T/F
描述: 在有效哈密顿量方法模块中常用。用于设置在分析完各种不等价相互作用项之后,是否计算若干构型的 \(\left\{h_{j}^{(i)}\right\}\) (定义见2.2.1节)并输出到 *.ene_symbol 文件中。这些构型可以是随机生成的,也可以是自定义的,这由“
local_mode.cal_para_method”设置项决定。案例:
Invariant.cal_para T
参数名称: local_mode.cal_para_method
默认值: 1
可选值: 1/4/5/6/9等(手册目前仅介绍最常用的1、5、6)
描述: 在有效哈密顿量方法模块中常用。用于设置采用哪种方式定义构型,可以自定义,也可以随机生成。最常用的设置选项有1、5和6。需要注意的是该项设置仅在“
Invariant.cal_para”取T时生效;而在“Invariant.use_alamode_IFC”取T(缺省值为F)时将自动设置为9(全原子模型)。设置值6是用 distortion.pos (必要文件)和 distortion.MAGMOM (无自旋自由度时可省略)文件提供自定义的构型信息,并在这两个文件内直接提供扩胞后的数据;设置值5是在 PASP.input 文件中用“block local_mode.mode_amp”提供自定义的构型信息,扩胞是利用“block SuperCell”设置项或 cell.str 文件完成的;设置值1是自动随机生成(也支持有序生成)多组构型,它也是通过“block SuperCell”设置项或 cell.str 文件完成扩胞。案例:
local_mode.cal_para_method 1
参数名称: Invariant.use_alamode_IFC
默认值: F
可选值: T/F
描述: 在有效哈密顿量方法模块中可能用到(目前不常用)。用于设置是否采用全原子模型。
案例:
Invariant.use_alamode_IFC F
参数名称: local_mode.nstr_random
默认值: 100
可选值: 非负整数
描述: 在“local_mode.cal_para_method”取1时,用于设置随机产生的构型数。在随机生成时,自旋自由度按模长为1随机生成方向,而局域声子模式和应变需要在“
block local_mode.mode_range”所设置的取值范围内随机取值。需要注意的是,只有相互作用分析中考虑到应变相关项时才会在随机生成数据时产生随机的应变。案例:
local_mode.nstr_random 150
参数名称: local_mode.generate_ordered_str
默认值: F
可选值: T/F
描述: 在“local_mode.cal_para_method”取1时,用于设置是否自动补充产生若干有序构型(上一设置项提到的随机构型编号在前,这里的有序构型编号在后)。取T时,有序构型按如下规则产生,实际产生的有序构型数常常难以事先估计:首先产生仅单个模式有值的若干构型(即其他模式赋零值),有值的模式大小为 \(i*1.5*u_{\max}/(num-1)\) ( \(u_{max}\) 和 \(num\) 为“
block local_mode.mode_range”中设置的相应模式的“最大值”和“分段数”, \(i\) 取值从1到 \(num-1\) );另外也会产生两个、多个模式有值的情形,有值的模式大小为 \(i * u_{\max } /(n u m-1)\) ( \(i\) 取值从1到 \(num-1\) )。该功能有时会生成部分重复或等价构型,因此并不是很常用。案例:
local_mode.generate_ordered_str F
参数名称: local_mode.mode_range
默认值: 对于各模式,最小值的缺省值为0(注意不是最大值的相反数);最大值的缺省值一般为0.04,但应变对应的最大值为0.02;分段数缺省值为4。
可选值: 最大值、最小值为实数,分段数为正整数
描述: 在“local_mode.cal_para_method”取1时,用于设置随机构型的取值范围,以及产生有序构型的相关设置信息。共需“局域模式数+6”行:其中局域模式数应与测试运行时名为 local_mode-*.xsf (*处为编号)的输出文件的个数一致,而这个个数未必与“block local_mode.mode_definition”部分定义的局域模式数一致(因为PASP软件可能会根据对称性分析补充对称等价的局域模式);“+6”部分对应应变的六个自由度。每行内容可以有两种格式:第一种,“最大值 分段数”(此时最小值取缺省值0);第二种,“最大值 最小值 分段数”。这两种格式可以混用。对于生成有序构型所需的“最大值”和“分段数”两个数据,直接从这里获取,产生有序构型的规则详见“
local_mode.generate_ordered_str”设置项介绍。对于随机生成构型的部分,各模式先从各自对应的[最小值,最大值]均匀随机取值;在“local_mode.randstr_randsign”为T(缺省值为T)时再随机取正负号,否则不随机取正负号。在案例1中,若“local_mode.randstr_randsign”取T,则前三种局域模式会在[0,0.276]均匀随机取值后再随机取正负号,这等价于在[-0.276,0.276]均匀随机取值;反之,若使用“local_mode.randstr_randsign F”,则前三种局域模式会在[0,0.276]均匀随机取值。对于案例2,常搭配“local_mode.randstr_randsign”取F来使用,以便更自由地设置各模式的取值范围,对于该例,第四至六种模式(对应前三种应变模式)会在[-0.02,0.03]均匀随机取值,而最后三种模式固定取值0.0(需要固定某模式取值时,只需要将最大值和最小值设成相等)。案例1:
%block local_mode.mode_range 0.276 11 0.276 11 0.276 11 0.025 2 0.025 2 0.025 2 0.025 2 0.025 2 0.025 2 %endblock local_mode.mode_range
案例2:
%block local_mode.mode_range 1.0 -1.0 2 1.0 -1.0 2 1.0 -1.0 2 0.03 -0.02 2 0.03 -0.02 2 0.03 -0.02 2 0.0 0.0 2 0.0 0.0 2 0.0 0.0 2 %endblock local_mode.mode_range
参数名称: local_mode.randstr_randsign
默认值: T
可选值: T/F
描述: 参见上一设置项,在“
local_mode.cal_para_method”取1时,对于随机生成构型的部分,各模式先从各自对应的[最小值,最大值]均匀随机取值;在“local_mode.randstr_randsign”为T(缺省值为T)时再随机取正负号,否则不随机取正负号。案例:
local_mode.randstr_randsign T
参数名称: block local_mode.mode_amp
默认值: 对所有自由度全部赋0
可选值: 实数
描述: 当“
local_mode.cal_para_method”设置值为5时,可利用“block local_mode.mode_amp”生成自定义的构型,如案例所示。
备注
这里需要提供“超胞”中所有相关局域模式的信息,比如示例中实际上提供了2*2*2超胞中所有需考虑的局域模式的信息。这里超胞是通过“
block SuperCell”设置项和 cell.str 文件决定的;由于“block SuperCell”扩胞所得各原子坐标通常难以预先确定,这里通常推荐直接在 cell.str 中提供超胞,以便直接确定超胞中所有原子的坐标。案例注释中“第几种模式”指属于该原子的第几种模式(比如属于某个原子的模式只有两种,那么只能取值1或2),而不是所有模式中的第几种。对于局域声子模式,可能某种模式中包含多个原子的位移信息,我们规定在“block local_mode.mode_definition”的模式定义中第一行是哪种原子,就称这个模式属于这种原子;考虑到扩胞等因素,这种原子可能有多个等价的位置,具体的某个模式应当属于某个具体等价位置的原子。
对于自旋模式需特别注意,软件将直接按照“block local_mode.mode_amp”的内容对模式大小赋值,不会再额外作归一化处理;为了内部逻辑统一,当设置自旋模式大小时,请务必确保每个自旋模式都是已经归一化的。
案例:
%block local_mode.mode_amp 24 #以下读取多少行含坐标的数据:笛卡尔坐标;第几种模式;模式大小 2.016548011745 2.016548011745 2.016548011745 1 0.21225237 2.016548011745 2.016548011745 2.016548011745 2 0 2.016548011745 2.016548011745 2.016548011745 3 0 2.016548011745 2.016548011745 6.049644035234 1 0.21225237 2.016548011745 2.016548011745 6.049644035234 2 0 2.016548011745 2.016548011745 6.049644035234 3 0 2.016548011745 6.049644035234 2.016548011745 1 0.21225237 2.016548011745 6.049644035234 2.016548011745 2 0 2.016548011745 6.049644035234 2.016548011745 3 0 2.016548011745 6.049644035234 6.049644035234 1 0.21225237 2.016548011745 6.049644035234 6.049644035234 2 0 2.016548011745 6.049644035234 6.049644035234 3 0 6.049644035234 2.016548011745 2.016548011745 1 0.21225237 6.049644035234 2.016548011745 2.016548011745 2 0 6.049644035234 2.016548011745 2.016548011745 3 0 6.049644035234 2.016548011745 6.049644035234 1 0.21225237 6.049644035234 2.016548011745 6.049644035234 2 0 6.049644035234 2.016548011745 6.049644035234 3 0 6.049644035234 6.049644035234 2.016548011745 1 0.21225237 6.049644035234 6.049644035234 2.016548011745 2 0 6.049644035234 6.049644035234 2.016548011745 3 0 6.049644035234 6.049644035234 6.049644035234 1 0.21225237 6.049644035234 6.049644035234 6.049644035234 2 0 6.049644035234 6.049644035234 6.049644035234 3 0 0.0 0.0 0.0 0.0 0.0 0.0 #额外的最后一行设置应变的值,全取零时可以省略此行 %endblock local_mode.mode_amp
3.1.7.8 Model find_J_path_sym 的其他设置¶
参数名称: block magnetic_or_ligand
默认值: 0
可选值: 0/1/2
描述: 在“Model find_J_path_sym”中用到。这里需指出各元素原子是磁性原子还是配位原子。1表示磁性原子,2表示配位原子,其他原子用0表示。以 \(BiFeO_{3}\) 为例,由于Fe是磁性原子取1,O是配位原子取2,Bi是其他原子取0,按Bi、Fe、O的顺序(顺序与block Z_values的内容一致)应分别取0、1、2。
案例:
%block magnetic_or_ligand 0 1 2v
3.1.7.9 Model Invariant 的其他设置¶
参数名称: Invariant.type
默认值: 1
可选值: 1/2/3/5/6
描述: 用于选定“Model Invariant”中分析不等价相互作用时的具体方法。本手册仅涉及选项2,即分析自定义的局域模式之间的不等价相互作用。其他选项不常用,这里不展开介绍。
案例:
Invariant.type 2
参数名称: local_mode.general_model
默认值: F
可选值: T/F
描述: 用于设置“Model Invariant”中分析不等价相互作用时是否采用通用方法。常选T。本手册仅涉及选T的情形;选F时仅适用于钙钛矿(perovskite)情形,现已不常用。
案例:
local_mode.general_model T
参数名称: local_mode.full_atomic
默认值: F
可选值: T/F
描述: 用于设置“
Model Invariant”中分析不等价相互作用时是否采用全原子模型(即考虑所有原子的全部位移自由度)。常选F。此功能可以被自定义局域模式的方法代替。案例:
local_mode.full_atomic F
参数名称: Invariant.debug
默认值: F
可选值: T/F
描述: 用于设置“
Model Invariant”中是否采用debug模式,debug模式下会在标准输出中提供更多相关数据信息。T和F都常选。追求计算效率时请设置成F。案例:
Invariant.debug F
3.1.8 全局结构搜索常用设置项¶
本节介绍全局结构搜索中常用的独有设置项。由于目前用的最多的是GA方法(遗传算法),所以这里主要涉及GA的相关设置项。
参数名称: GA.population_size
默认值: 0
可选值: 非负整数
描述: 用于设置在遗传算法中每一代的种群大小。
案例:
GA.population_size 20
参数名称: GA.max_generation
默认值: 0
可选值: 非负整数
描述: 用于设置遗传算法的迭代次数。
案例:
GA.max_generation 10
参数名称: save_str.nsave_str
默认值: 10
可选值: 非负整数
描述: 用于设置程序最终输出的低能结构数量。
案例:
save_str.nsave_str 20
参数名称: GA.perturbation
默认值: F
可选值: T/F
描述: 用于设置是否开启微扰方法。
案例:
GA.perturbation T
参数名称: GA.Pher
默认值: 0.85
可选值: 0~1之间的实数
描述: 用于设置遗传算法交叉的概率。
案例:
GA.Pher 0.85d0
参数名称: GA.Pmut
默认值: 0.10
可选值: 0~1之间的实数
描述: 用于设置遗传算法突变的概率。
案例:
GA.Pmut 0.10d0
参数名称: GA.lchk_mut
默认值: T
可选值: T/F
描述: 用于设置是否检查突变后的结果并舍弃其中不合理的结构。
案例:
GA.lchk_mut T
参数名称: str.init_sym
默认值: F
可选值: T/F
描述: 用于设置结构的初始对称性。
案例:
str.init_sym T
参数名称: GA.symmetrize_str
默认值: F
可选值: T/F
描述: 用于设置是否对结构做对称化处理。
案例:
GA.symmetrize_str T
参数名称: GA.parallel
默认值: F
可选值: T/F
描述: 用于设置是否使用并行方法。
案例:
GA.parallel T
参数名称: GA.useBCM
默认值: T
可选值: T/F
描述: 用于设置在判断结构相似性时是否使用BCM方法。
案例:
GA.useBCM T
参数名称: GA.tol_BCM
默认值: 0.01
可选值: 非负实数
描述: 用于设置BCM方法中所能容忍的误差大小。
案例:
GA.tol_BCM 0.01d0
参数名称: GA.pressure
默认值: 0.0
可选值: 非负实数
描述: 用于设置外界压力大小,单位为GPa。
案例:
GA.pressure 0.0d0
参数名称: GA.gen_ran_str_sym
默认值: F
可选值: T/F
描述: 用于设置是否使用随机空间群方法来生成初始结构,做全局结构搜索,并生成空间群为GA.spg_front到GA.spg_rear的随机结构。
案例:
GA.gen_ran_str_sym T
参数名称: GA.spg_front
默认值: 1
可选值: 1~230之间的正整数
描述: 用于设置结构搜索中的起始空间群号。
案例:
GA.spg_front 1
参数名称: GA.spg_rear
默认值: 230
可选值: 1~230之间的正整数
描述: 用于设置结构搜索中的终点空间群号。
案例:
GA.spg_rear 230
参数名称: GA.magnetic
默认值: F
可选值: T/F
描述: 用于设置在结构搜索中是否考虑磁性自由度。
案例:
GA.magnetic T
参数名称: GA.random_magnetic
默认值: T
可选值: T/F
描述: 如果参数值为T,则随机生成磁构型;如果参数值为F,则按照磁空间群生成磁构型。
案例:
GA.random_magnetic F
参数名称: GA.lAFM_GA
默认值: F
可选值: T/F
描述: 如果参数值设为T,则程序仅考虑AFM态(反铁磁态)。
案例:
GA.lAFM_GA T
参数名称: GA.lmut_mag_GA
默认值: F
可选值: T/F
描述: 用于设置是否使体系的磁构型发生突变。
案例:
GA.lmut_mag_GA T
参数名称: GA.flip_spin_rate
默认值: 0.2
可选值: 0~1之间的实数
描述: 用于设置磁矩发生突变的概率。
案例:
GA.flip_spin_rate 0.25d0
参数名称: GA.ldiff_str_with_mag_GA
默认值: F
可选值: T/F
描述: 如果参数值为T,则仅当两个结构同时满足位置构型和磁构型的一致性时,程序才会视其为相同的结构。
案例:
GA.ldiff_str_with_mag_GA T
参数名称: GA.lread_OUTCAR_mag
默认值: F
可选值: T/F
描述: 用于设置是否从 OUTCAR 文件中读取磁性相关的信息并更新体系的磁构型。
案例:
GA.lread_OUTCAR_mag F
参数名称: GA.fixlattice
默认值: F
可选值: T/F
描述: 用于设置是否固定晶格。
案例:
GA.fixlattice F
参数名称: GA.fix_cell
默认值: T
可选值: T/F
描述: 用于设置是否固定晶胞。
备注
注意:当参数 GA.fixlattice 设为T时,参数 GA.fix_cell 亦为T。.
案例:
GA.fix_cell F
参数名称: GA.biaxial_strain
默认值: F
可选值: T/F
描述: 用于设置是否施加面内的应变,即保持面内晶格常数固定。
案例:
GA.biaxial_strain T
参数名称: block GA.lat_fix_2D_Ang
默认值: 缺省时将自动设置该变量为 “
block LatticeVectors”(参见3.1.3.4节)中给出的前两行数据。可选值: 6个非负实数
描述: 用于设置固定的面内晶格常数。
案例:
%block GA.lat_fix_2D_Ang 5.5225 0.0 0.0 0.0 5.5225 0.0 %endblock GA.lat_fix_2D_Ang
3.1.9 紧束缚模型方法常用设置项¶
本节介绍紧束缚模型方法中常用的独有设置项。
参数名称: USE_Slater_Koster_Model
默认值: F
可选值: T/F
描述: 是否使用Slate-Koster模型得到
hopping参数,是则使用T,不使用S-K模型而直接手动输入所有hopping参数时选用F。案例:
USE_Slater_Koster_Model T
参数名称: overlap.distance
默认值: 100000
可选值: 正实数
描述: 交叠距离,略大于考虑跃迁的成键键长即可。单位Bohr。
案例:
overlap.distance 4.1
参数名称: Different_hop_path
默认值: 在S-K TB中为1,自定义TB中手动输入hopping参数时为0
可选值: 非负整数
描述: 在自定义TB中,每对发生跃迁的元素为一条hop_path;在S-K TB中,每对跃迁壳层组合为一条hop_path。
案例:
- 在自定义TB中,考虑石墨烯中C-C跃迁,则hop_path为1 Different_hop_path 1 - 在S-K TB中,考虑Ni 3d轨道与O 2p跃迁,以及Ni 4s轨道与O 2p跃迁,则hop_path为2。 Different_hop_path 2
参数名称: Hop_Parameters_specified_using_site
默认值: F
可选值: T/F
描述: 选用T则以位矢之差表示跃迁路径,若该项选用F,则
Hop_Parameters_specified_using_dis一项必须为T。
备注
Hop_Parameters_specified_using_site 与 Hop_Parameters_specified_using_dis 二者必须一个为T,另一个为F。使用site时跃迁信息以不同的原子编号作区分,使用distance时以不同的元素编号作区分。推荐使用Hop_Parameters_specified_using_dis。
案例:
Hop_Parameters_specified_using_site T
参数名称: Hop_Parameters_specified_using_dis
默认值: F
可选值: T/F
描述: 选用T则以原子间距离表示跃迁路径,若该项选用F,则
Hop_Parameters_specified_using_site一项必须为T。
备注
Hop_Parameters_specified_using_site 与 Hop_Parameters_specified_using_dis 二者必须一个为T,另一个为F。使用site时跃迁信息以不同的原子编号作区分,使用distance时以不同的元素编号作区分。推荐使用Hop_Parameters_specified_using_dis。
案例:
Hop_Parameters_specified_using_dis T
参数名称: TB.complex_hop
默认值: F
可选值: T/F
描述: TB跃迁参数是否选用复数,若选用复数则设置为T,
block Hop_parameters中每个跃迁参数以(r,i)形式表示,其中r为实部数值,i为虚部数值。当使用S-K TB时缺省此项。案例:
TB.complex_hop F
参数名称: block Hop_Parameters
默认值: 无默认值,使用自定义TB时不可缺省
可选值: 见描述
描述: 输入自定义TB的hopping参数信息,若
Hop_Parameters_specified_using_site为T(案例1),第一行依次输入发生跃迁的两个原子编号,两原子间的位矢差的x y z分量;另起一行输入跃迁矩阵,两原子中第一个原子的轨道数作为行数,第二个原子的轨道数作为列数(注意这里的轨道数应当与block Orbitals中指定的各元素轨道数一致)。若Hop_Parameters_specified_using_dis为T(案例2),第一行依次输入发生跃迁的元素在 cell.str 中对应编号,以及元素间成键长度(略微大于键长也可),另起一行输入两元素间跃迁矩阵,行数为前面元素轨道数,列数为后面元素轨道数(注意这里的轨道数也应当与block Orbitals中指定的各元素轨道数一致)。另注意,TB.complex_hop为T时,这里每个跃迁参数以(r,i)形式表示,其中r为实部数值,i为虚部数值。当使用S-K TB时缺省此项。案例1:
考虑一号原子轨道数为3,二号原子为2,则 Hop_Parameters_specified_using_site T Hop_Parameters_specified_using_dis F %block Hop_Parameters 1 2 0.2 0.3 0.5 # ia1,ia2, cell_diff 0 -1.5 2 0 0 1.3 %endblock Hop_Parameters
案例2:
考虑一号元素轨道数为3,二号元素为2,则 Hop_Parameters_specified_using_site F Hop_Parameters_specified_using_dis T %block Hop_Parameters 1 2 2.1 # is1,is2,distance 0 -1.5 2 0 0 1.3 %endblock Hop_Parameters
参数名称: block Slater_Koster_Hop_Parameters
默认值: 无默认值,使用SK TB时不可缺省
可选值: 见描述
描述: 输入SK TB的hopping参数信息,若
Hop_Parameters_specified_using_site为T(案例1),第一行依次输入发生跃迁的两个原子编号,两原子间的位矢差的x y z分量;第二行输入跃迁壳层组合数,数值等于Different_hop_path项;第三行依次输入第一个原子跃迁壳层的主量子数、角量子数,第二个原子跃迁壳层的主量子数、角量子数;第四行输入相应的S-K TB跃迁积分项(p轨道与p轨道间为 \(V_{ppσ} V_{ppπ}\) , p轨道与d轨道间为 \(V_{pdσ} V_{pdπ}\) ,p轨道与f轨道间为 \(V_{pfσ} V_{pfπ}\) )等数值,根据结构对称性,表示跃迁的不同矩阵元是这些数值的不同线性组合形式,这一组合过程将由程序完成。若Hop_Parameters_specified_using_dis为T(案例2),则第一行依次输入原子种类序数,原子间距离;其余行不变。
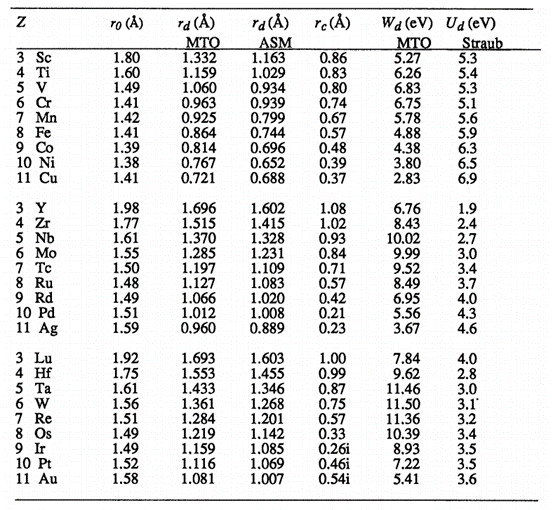
根据W.A.Harrison所著“Electronic structure and the properties of solids - The Physics of the Chemical Bond”一书,不同体系的 \(V_{ppσ}\) 等参数可进一步近似为轨道间普适常量 \(η\) 除以跃迁距离的平方,根据此可给出 \(V_{ppσ}\) 等参数的初始值。具体为:对于 \(ss,sp,pp:\mathrm{V}_{\mathrm{ll}^{\prime} \mathrm{m}}=\eta_{\mathrm{ll}^{\prime} \mathrm{m}} \frac{\hbar^2}{\mathrm{~m}_{\mathrm{e}} \mathrm{d}^2}\),对于 \(sd,pd,\mathrm{V}_{\mathrm{ll}^{\prime} \mathrm{m}}=\eta_{\mathrm{ll}^{\prime} \mathrm{m}} \frac{\hbar^2 \mathrm{r}_{\mathrm{d}}^{3 / 2}}{\mathrm{~m}_{\mathrm{e}} \mathrm{d}^{7 / 2}}\) ,对于 \(dd,\mathrm{V}_{\mathrm{ll}^{\prime} \mathrm{m}}=\eta_{\mathrm{ll}^{\prime} \mathrm{m}} \frac{\hbar^2 \mathrm{r}_{\mathrm{d}}^3}{\mathrm{~m}_{\mathrm{e}} \mathrm{d}^5}\) ,式中 \(m_e\) 为电子质量,\(d\) 为跃迁原子间距离(键长),\(r_{d}\) 为d态半径(d-state radii)。 \(\eta_{ss\sigma}=-1.40\), \(\eta_{sp\sigma}=1.84\), \(\eta_{pp\sigma}=3.24\), \(\eta_{pp\pi}=-0.81\), \(\eta_{sd\sigma}=-3.16\), \(\eta_{pd\sigma}=-2.95\), \(\eta_{pd\pi}=1.36\), \(\eta_{dd\sigma}=-16.2\), \(\eta_{dd\pi}=8.75\), \(\eta_{dd\delta}=-2.39\);\(r_d\) 取值表如下,其中MTO指Anderson与Jepsen使用Muffin-Tin-Orbital理论推导所得,ASM指Straub与Harrison使用Atomic-Surface Method推导所得。
备注
由上述数据推导出的跃迁参数数值可作为初步的大致合理值使用,对于具体体系,跃迁参数可根据初始值结果进一步优化。或者可以通过调节跃迁参数数值大小来理解不同轨道跃迁对各项性质的影响。
案例1:
Hop_Parameters_specified_using_site T Hop_Parameters_specified_using_dis F %block Slater_Koster_Hop_Parameters 1 3 0.2 0.3 0.5 # ia1,ia2, cell_diff 1 # hop pairs 2 1 3 3 # n1 l1 n2 l2 0.1 0.2 # t(l1, l2, m) %endblock Slater_Koster_Hop_Parameters
案例2:
Hop_Parameters_specified_using_site F Hop_Parameters_specified_using_dis T %block Slater_Koster_Hop_Parameters 1 2 2.0 # is1, is2, distance 1 # nl pairs 2 1 3 3 # n1 l1 n2 l2 0.1 0.2 # t(l1, l2, m) %endblock Slater_Koster_Hop_Parameters
参数名称: block Orbitals
默认值: 无默认,不可缺省
可选值: 略,见描述
描述: 此模块输入轨道在位能信息(单位eV),使用自定义TB时(案例1),第一行给出 cell.str 中的元素编号1,及其轨道数(轨道数目及轨道的物理含义由研究者所使用的TB模型决定),第二行给出这些轨道上在位能大小,第三行给出元素编号2及其轨道数,以此类推。使用S-K TB时(案例2),第一行给出元素序号1,以及该元素考虑hopping壳层的轨道数,第二行给出这些轨道上电子在位能的数值,第三行给出元素序号2,以及该元素考虑hopping壳层的轨道数,第四行给出这些轨道上电子在位能的数值。其它元素以此类推。输入时各轨道顺序为:p轨道: \(p_{x}\) , \(p_{y}\) , \(p_{z}\) ;d轨道: \(d_{z2-r2}\) , \(d_{x2-y2}\) , \(d_{yz}\) , \(d_{zx}\) , \(d_{xy}\) ;f轨道: \(f_{xyz}\) , \(f_{x3}\) , \(f_{y3}\) , \(f_{z3}\) , \(f_{x(y2-z2)}\) , \(f_{y(z2-x2)}\) , \(f_{z(x2-y2)}\) 。在位能数值可由各个轨道PDOS的主峰位置大致估计。
案例1:
#不使用S-K TB %block Orbitals 1 3 0.5 0.5 0.5 2 3 -1.2 -1.2 -1.2 %endblock Orbitals
案例2:
#使用S-K TB %block Orbitals 1 5 0.7 0.7 -0.2 -0.2 -0.2 2 3 -1.7 -1.7 -1.7 %endblock Orbitals
参数名称: block orbitals_nl
默认值: 无,不可缺省
可选值: 见描述
描述: 壳层信息,第一行为元素种类1,及其考虑的壳层数,下面每行列举所考虑壳层对应的主量子数及角量子数,再另起一行写元素种类2,及其考虑的壳层数,以及所考虑壳层对应的主量子数及角量子数。
案例: (Ni 3d 4s轨道以及O 2p轨道)
%block orbitals_nl 1 2 #第一种元素 考虑两个轨道 3 2 #3d轨道的n l 4 0 #4s轨道的n l 2 1 #第二种元素 考虑一个轨道 2 1 #2p轨道的n l %endblock orbitals_nl
参数名称: spin_noncollinear
默认值: F
可选值: T/F
描述: 是否开启非共线。
案例:
spin_noncollinear T
参数名称: Sn_basis
默认值: F
可选值: T/F
描述:
Sn_basis项决定了自旋量子化轴的z轴方向,若设置为F,则其始终沿晶胞c轴方向,若设置为T,则其为自旋所指方向。这一差异会导致在展开哈密顿量时,SOC项的形式产生差异,进而使得哈密顿量矩阵形式产生差异。具体如下。若
Sn_basis设置为F,则SOC哈密顿量展开为:
若
Sn_basis设置为T,则SOC哈密顿量展开为:
案例:
Sn_basis F
参数名称: nspin_directions_set
默认值: 0
可选值: 正整数
描述: 设定具有磁矩的原子数目。
案例:
nspin_directions_set 2
参数名称: block spin_directions_set
默认值: 无
可选值: 见描述
描述: 当
nspin_directions_set设置为0时,此项不设置,不为零时,每行按原子序号,输入其上自旋方向。案例:
%block spin_directions_set 1 -0.707107 0.707107 0.000000 #1号原子及其自旋方向 2 1.000000 0.000000 0.000000 #2号原子及其自旋方向 %endblock spin_directions_set
参数名称: nsites_SOC
默认值: 0
可选值: 正整数
描述: 开启SOC的原子的数目。
案例:
nsites_SOC 2
参数名称: block magnitude_SOC
默认值: 无
可选值: 见描述
描述: 给每个开启SOC的原子设定SOC强度,数值可借由公式 \(\left(g_s-1\right) \frac{1}{2} \frac{1}{4 \pi \varepsilon_0} \frac{Z e^2}{r^3} \frac{1}{m_e^2 c^2}\) 进行估算。
案例:
%block magnitude_SOC 1 0.3 #1号原子,对应的SOC强度λ为0.3eV 2 0.03 #2号原子,对应的SOC强度λ为0.03eV %endblock magnitude_SOC
参数名称: TB.U
默认值: 0
可选值: 正实数
描述: 描述Hubbard排斥作用的U值大小(单位eV),与DFT计算中U值相近。
案例:
TB.U 3
参数名称: use_rotation_matrix
默认值: F
可选值: T/F
描述: 是否用旋转矩阵处理角动量,在使用SK TB时此项必须设置为T。
案例:
use_rotation_matrix T
参数名称: TB.additional_H
默认值: F
可选值: T/F
描述: 若需要额外手动加入哈密顿量(如考虑外场时),设置为T,并在原来两个输入文件之外,增加要添加的数值矩阵文件“ Hmat_add.dat ”,以正- 八面体六配位环境下的单Ni原子示例,考虑SOC后,3d共有10个轨道,因此添加的哈密顿量矩阵也是10*10矩阵, Hmat_add.dat 文件具体内容参见2.4.2节。
备注
添加矩阵的大小应和PASP生成矩阵大小相同;
添加矩阵时,各轨道对应的矩阵元要注意按照PASP TB的轨道顺序进行添加;
由于Fortran读取复数的语法规则,括号内实部与虚部之间需要逗号隔开;
添加的矩阵应是厄密的,PASP会对矩阵的厄密性进行检查。
案例:
TB.additional_H T
参数名称: block kgrid_Monkhorst_Pack
默认值: 无
可选值: 见描述
描述: K点网格设置,前面3*3矩阵给出网格,最后一列表示网格偏移量
案例:
%block kgrid_Monkhorst_Pack 4 0 0 0.2 0 4 0 0.2 0 0 1 0.2 %endblock kgrid_Monkhorst_Pack #表示4*4*1的K点网格,最后一列为各方向偏移0.2
参数名称: block DensityOfStates
默认值: 无
可选值: 见描述
描述: 态密度计算设置,输入按顺序为最低能、最高能、展宽、能量区间内取点数以及单位(eV或Hartree)。
案例:
%block DensityOfStates 0.00 0.00 0.200 1000 Hartree %endblock DensityOfStates
参数名称: BandLinesScale
默认值: 无
可选值: pi/a或ReciprocalLatticeVectors
描述: 能带计算时高对称点表示方式,pi/a即用倒格矢指数上pi/a倍数表示,ReciprocalLatticeVectors即用倒格矢的分数坐标表示。
案例:
BandLinesScale ReciprocalLatticeVector
参数名称: block BandLines
默认值: 无
可选值: 见描述
描述: 能带计算设置,第一列表示路径上取点数目,第二列至第三列分别表示所选高对称点的分数坐标,最后一列为高对称点符号。使用时在block之前应添加“
BandLinesScale”输入来设置高对称点表示方法。案例1:
BandLinesScale ReciprocalLatticeVectors %block BandLines 1 0.000000000 0.000000000 0.000000000 \Gamma 20 0.666666667 0.333333333 0.000000000 K 10 0.500000000 0.000000000 0.000000000 M 20 0.000000000 0.000000000 0.000000000 \Gamma 15 0.000000000 0.000000000 0.500000000 A 20 0.666666667 0.333333333 0.500000000 H 10 0.500000000 0.000000000 0.500000000 L %endblock BandLines #以倒格矢分数坐标表示高对称点,能带绘制路径: Gamma点-- K点-- M点-- Gamma点-- A点-- H点-- L点,路径上分别取20、10、20、15、20、10个点
案例2:
BandLinesScale pi/a %block BandLines 1 0.000 0.000 0.000 \Gamma 20 2.000 0.000 0.000 H 15 1.000 1.000 0.000 N 15 0.000 0.000 0.000 \Gamma 20 1.000 1.000 1.000 P 10 1.000 1.000 0.000 N 10 1.000 1.000 1.000 P 20 2.000 2.000 2.000 H %endblock BandLines #以pi/a倍数表示高对称点,能带绘制路径: Gamma点-- H点-- N点-- Gamma点-- P点-- N点-- P点-- H点,路径上分别取20、15、15、20、10、10、20个点
3.1.10 自旋序诱导铁电性统一极化模型常用设置项¶
本节介绍自旋序诱导铁电性统一极化模型中常用的独有设置项。
参数名称: GKNB.symP
默认值: F
可选值: T/F
描述: 是否在程序里根据晶体结构对称性来对称化极化参数。
案例:
GKNB.symP T
参数名称: block GKNB_inter_site
默认值: 分量全部为0
可选值: 分量为实数
描述: 设定格点间项极化参数矩阵 \(\vec{P}_{12}^{\alpha \beta}\) (定义见2.5.1节)。其中第一行给出了不等价离子对的个数。接下来需要对每一个不等价离子对给出离子位置的笛卡尔坐标(Å为单位),采用的局域坐标系(通常为单位矩阵),和 \(\vec{P}_{12}^{\alpha \beta}\) 数据。\(\vec{P}_{12}^{\alpha \beta}\) 数据部分共9行,第1行是 \(\vec{P}_{12}^{xx}\) 的三个分量(案例中注释为xx),第2行是 \(\vec{P}_{12}^{xy}\) y的三个分量(案例中注释为xy),以此类推。若有多组数据(即第一行内容大于1),则换行继续添加其他组数据的内容即可,两组数据之间不空行。
案例:
%block GKNB_inter_site 1 #不等价离子对的个数 6.184071509801 6.184071509801 6.184071509801 #Fe2 4.638053632351 6.184071509801 9.276107264702 #Fe35 1 0 0 #局域坐标系x轴 0 1 0 #局域坐标系y轴 0 0 1 #局域坐标系z轴 0.001254 0.00213 0.002374 #xx 0 0 0 #xy 0 0 0 #xz 0 0 0 #yx 0.001254 0.00213 0.002374 #yy 0 0 0 #yz 0 0 0 #zx 0 0 0 #zy 0.001254 0.00213 0.002374 #zz %endblock GKNB_inter_site
参数名称: block GKNB_single_site
默认值: 分量全部为0
可选值: 分量为实数
描述: 设定单格点项极化参数矩阵 \(\vec{P}_{i}^{\alpha \beta}\) (定义见2.5.1节)。其中第一行给出了不等价单格点的个数。接下来需要对每一个不等价单格点给出离子位置的笛卡尔坐标(Å为单位),采用的局域坐标系(通常为单位矩阵),和 \(\vec{P}_{i}^{\alpha \beta}\) 数据。\(\vec{P}_{i}^{\alpha \beta}\) 数据部分共6行,第1行是 \(\vec{P}_{i}^{xx}\) 的三个分量(案例中注释为xx),第2行是 \(\vec{P}_{i}^{yy}\) 的三个分量(案例中注释为yy),第3行是 \(\vec{P}_{i}^{zz}\) 的三个分量(案例中注释为zz),第4行是 \(\vec{P}_{i}^{xy} = \vec{P}_{i}^{yx}\) 的三个分量(案例中注释为xy=yx),以此类推。若有多组数据(即第一行内容大于1),则换行继续添加其他组数据的内容即可,两组数据之间不空行。
案例:
%block GKNB_single_site 1 6.184071509801 6.184071509801 6.184071509801 #Fe2 1 0 0 #局域坐标系x轴 0 1 0 #局域坐标系y轴 0 0 1 #局域坐标系z轴 0 #Pxx 0 #Pyy 0 #Pzz 0 #Pxy=Pyx 0 #Pxz=Pzx 0 #Pyz=Pzy %endblock GKNB_single_site
参数名称: block GKNB_local_axis
默认值: 单位矩阵
可选值: 正交矩阵
描述: 设定新的局域坐标系(通常为单位矩阵)。当与设定 \(\vec{P}_{12}^{\alpha \beta}\) 、\(\vec{P}_{i}^{\alpha \beta}\) 时采用的局域坐标系不一致时,将采用这里设定的坐标系,并对 \(\vec{P}_{12}^{\alpha \beta}\) 、\(\vec{P}_{i}^{\alpha \beta}\) 作适当变换(分量变换到新坐标系下的形式)。
案例:
%block GKNB.local_axis 1 0 0 0 1 0 0 0 1 %endblock GKNB.local_axis
参数名称: block GKNB.spiral
默认值: F
可选值: T/F
描述: 是否对自旋序附加spiral(螺旋)。选T时,利用“block GKNB.qvec”(定义q,采用倒格子基矢下的分数坐标形式)和“block GKNB.spiral_plane_vec”(定义 \(e_1\) 和 \(e_2\),采用笛卡尔坐标形式)定义附加的螺旋序。此时位于r(分数坐标形式)、原自旋矢量为S的磁性原子,相位变为 \(\varphi=\operatorname{acos}\left(\frac{S_z}{|S|}\right)+2 \pi \boldsymbol{q} \cdot \boldsymbol{r}\),附加螺旋序之后的自旋矢量变为 \(|\boldsymbol{S}|\left(\boldsymbol{e}_1 \cos \varphi+\boldsymbol{e}_2 \sin \varphi\right)\)
案例:
GKNB.spiral T
参数名称: block GKNB.qvec
默认值: 0
可选值: 分量为实数
描述: 采用倒格子基矢下的分数坐标形式。该矢量记为q。
案例:
%block GKNB.qvec 0.004500000000 0.004500000000 0.000000000000 %endblock GKNB.qvec
参数名称: block GKNB.spiral_plane_vec
默认值: 需要用到时不可缺省
可选值: 两行分别为相互正交的两个单位方向向量
描述: 采用笛卡尔坐标形式,提供相互正交的两个单位方向向量,分别记为 \(e_1\) 和 \(e_2\) 。
案例:
%block GKNB.spiral_plane_vec 0 1 0 0 0 -1 %endblock GKNB.spiral_plane_vec
参数名称: spin_lat.spin_force
默认值: F
可选值: T/F
描述: 是否计算自旋序导致的离子受力。
案例:
spin_lat.spin_force T
参数名称: spin_lat.Lspin_int_only
默认值: T
可选值: T/F
描述: 是否仅考虑自旋自由度。选T时,忽略离子位移自由度和应变自由度。
案例:
spin_lat.Lspin_int_only F
参数名称: spin_lat.Lstrain_only
默认值: F
可选值: T/F
描述: 是否仅考虑晶格应变的影响。选T时,忽略离子位移的影响。
案例:
spin_lat.strain_only T
参数名称: spin_lat.spin_int_stress
默认值: F
可选值: T/F
描述: 是否计算自旋序导致的晶格应力。
案例:
spin_lat.spin_int_stress T
参数名称: phonopy_force_constant
默认值: F
可选值: T/F
描述: 是否读入phonopy给出的力常数文件。
案例:
phonopy_force_constant T
参数名称: phon.lasr
默认值: F
可选值: T/F
描述: 是否依据ASR(acoustic sum rule)修正力常数。
案例:
phon.lasr F
参数名称: phon.sym_born_chg
默认值: T
可选值: T/F
描述: 是否对称化给定的波恩有效电荷张量。
案例:
phon.sym_born_chg T
3.1.11 线性自旋波色散计算常用设置项¶
本节介绍线性自旋波的色散计算中常用的独有设置项。
参数名称: number_of_qpoints
默认值: 1
可选值: 正整数
描述: PASP每次计算布里渊区1条线段上的自旋波色散,本设置项代表这条线段上q点的数量。
案例:
number_of_qpoints 1
参数名称: block qpoints.magnon
默认值: 需要用到时不可缺省
可选值: 坐标分量为实数
描述: PASP每次计算布里渊区1条线段上的自旋波色散,本设置项第一行代表这条线段的起始q点(q用以倒格矢展开的系数 \(q_i\) 表示:\(\boldsymbol{q}=\sum_i q_i \boldsymbol{b}_i\) ),第二行代表这条线段的终末q点。
案例:
%block qpoints.magnon 0.5 0.0 0.0 0.0 0.0 0.0 %endblock qpoints.magnon
3.2 输入/输出文件seed.in:随机数种子¶
这是个非必要的输入文件,用于提供随机数种子,需要两个整型数据,例如:
640183986 154385448
如果缺少该文件,软件将自动随机生成随机数种子,并输出到 seed.in 文件中。
这个文件的用处在于,当软件运行过程中涉及随机数时(例如蒙特卡洛模拟、随机生成构型等),如果希望在两次计算中得到完全相同的结果,可以通过使用相同的随机数种子实现。当软件运行遇到bug时,有时会需要用此文件固定随机数种子。
3.3 输入文件spin_exchange.dat¶
在“Model Spin_lattice_interaction”中用该文件提供相互作用参数的取值信息。
注意:该文件采用严格的逐行读取规则,不能任意空行或删除、添加行。
示例文件如下(#后面的内容为注释部分,无需写出;注意这里#号需要用空格或制表符与数据隔开;此外#号开头的首尾两行不算在文件内容之内):
#=========================================#
2 #共几组相互作用 #以下三行提供unit_cell.str的晶格信息
5.0523118545661250 0.0000000000000000 0.0000000000000000
0.0000000000000000 5.0523118545661250 0.0000000000000000
0.0000000000000000 0.0000000000000000 5.0523118545661250
1 0.0 -0.00017 0.00017 -0.00017 0.0 0.00017 0.00017 0.00017 0.0 1 1 -1.79817 0.72799 1.79817 -1.79817 0.72799 1.79817 #single ion
2 -0.02858 -0.0000255 0.00024 -0.00047 -0.0278 0.00059 0.0000033 0.0004984 -0.028 1 1 1.79817 3.25414 0.72799 0.72799 1.79817 3.25414 #J1
0 # no dJ/du, i.e., no spin-lattice interaction
0 # single site anisotropy
0 # DM
2 #共几组四阶点乘形式相互作用
1 1 -0.005885 1 1
1.79817 3.25414 0.72799 0.72799 1.79817 3.25414
2 2 0.002435 1 1
1.79817 3.25414 0.72799 -0.72799 -0.72799 -0.72799 3.25414 0.72799 1.79817
#=========================================#
注意: 在本文件中,相互作用参数取eV单位(假定自旋矢量无量纲);坐标统一采用笛卡尔坐标形式,单位埃。
第一部分:第一行提供一个整数,表示第一部分(即J矩阵部分)共有几组相互作用。二到四行提供原胞矢量信息(与 unit_cell.str 的相应内容一致)。其后每行依次提供各组不等价对的相互作用信息,这部分总的行数应与本文件第一行设置的数字一致。每行的内容是“第几组相互作用;J矩阵(逐行填写矩阵元,共9个数);哪两个编号的元素之间相互作用(共2个数,一般是相同的);代表对原子的笛卡尔坐标(共6个数)”。当提供的代表对原子坐标相同时,J矩阵部分应填写SIA矩阵(单离子各向异性矩阵)。这里提到的J矩阵和SIA矩阵的定义参见2.1.1节。
第二部分:提供dJ/du的信息。这部分不常用,通常写0。使用这部分的完整示例文件参见 “example_public/P_by_spin_order/ion_strain/input/spin_exchange.dat” ,该部分内容示例如下,这里仅支持非矩阵形式的各向同性的J。第一行提供一个整数,表示后续有几组数据(每组数据对应一种J值对各个原子位移偏导的信息)。之后每组信息按如下格式填写:第几组dJ/du信息、对应第几种J(编号与本文件第一部分定义顺序一致);之后的3×3矩阵提供扩胞后的基矢(单位Ang);其后一行提供一个数字,表示对于当前J,提供对于多少原子位置的偏导信息,例如160个原子(通常等于扩胞后胞内原子数);之后提供这160个原子的坐标(笛卡尔坐标系,单位Ang),再依次给出该J值对于各个原子坐标分量的偏导(eV/Ang)。
#=========================================#
3 # ndJ,后续提供几组dJ/du信息
1 1 #第几组dJ/du信息、对应第几种J
-6.441774129000 11.157480082400 9.245866623200
-6.441774129000 -11.157480082400 9.245866623200
6.441774128900 0.000000000000 4.622933311600
160
0.000000000000 0.000000000000 0.000000000000
-3.220887064500 -5.578740041200 4.622933311600
……(省略若干行)
0.000003250000 -0.000050750000 -0.000006250000
2 2 #第几组dJ/du信息、对应第几种J
……(省略若干行)
3 3 #第几组dJ/du信息、对应第几种J
……(省略若干行)
#=========================================#
第三部分:提供SIA(单离子各向异性)的信息,这部分内容可以用第一部分的J矩阵代替。不提供这部分数据时,写0即可。有数据时,先在这部分的第一行写这部分有几组数据,然后每组数据按如下格式写:第一行提供一个整数(可以写成编号,即这是第几组),一般为非负整数(但当提供负值的整数时,表示该代表原子的所有等价原子都采用完全相同的SIA矩阵,而不会根据实际情况作任何适当的旋转变换等操作,一般情况不会选用负值);第二至四行提供能够使SIA矩阵对角化的局域坐标系(相应的坐标轴称为x’y’z’ 轴,这三行依次提供x’ 轴、y’ 轴和z’ 轴的信息),假定对角化后SIA矩阵为diag(E,-E,A)的形式;第五行提供五个数,第一个数为A值(z’ 轴对应的对角元),第二个数为E值(x’ 轴对应的对角元,也是y’ 轴对应的对角元的相反数),第三至五个数为代表原子的笛卡尔坐标。不同组的数据之间只换行不空行。
第四部分:提供DM(Dzyaloshinskii-Moriya)相互作用(定义参见2.1.1节)的信息,这部分内容也可以用第一部分的J矩阵代替。不提供这部分数据时,写0即可。有数据时,先在这部分的第一行写这部分有几组数据,然后每组数据写一行信息,其中包括12个数:第一个数写编号(这是第几组DM相互作用),第二至四个数写DM相互作用的矢量分量(在笛卡尔坐标系下),第五至六个数写这是哪两个编号的元素之间相互作用(一般是相同的),最后六个数写两个代表原子的笛卡尔坐标。
最后的第五部分:提供四阶点乘相互作用的信息。先提供一个整数,表示这部分共有几组四阶点乘相互作用。每组四阶点乘相互作用的信息分两行写,其中第一行依次写“第几组;第几种类型;参数值;哪两个编号的元素之间相互作用(共2个数,一般是相同的)”。其中“第几种类型”包括以下情形:第1种,二体四阶 \((S_{1}⋅S_{2})^{2}\) ;第2种,三体四阶 \((S_{1}⋅S_{2})(S_{1}⋅S_{3})\) ;第3种,四体四阶 \((S_{1}⋅S_{2})(S_{3}⋅S_{4})\) 。每组的第二行填写涉及的代表簇(代表对)原子的坐标:第1种类型提供两个原子的坐标(共6个数);第2种类型依次提供 \(S_{1}\) 、 \(S_{2}\) 和 \(S_{3}\) 对应的三个原子的坐标(共9个数);第3种类型依次提供 \(S_{1}\) 、 \(S_{2}\) 、 \(S_{3}\) 和 \(S_{4}\) 对应的对应的四个原子的坐标(共12个数)。
注意:相互作用截断距离要取的足够大(由“ block fig.mdist ”设定,参见3.1.7.2节),以确保 spin_exchange.dat 文件中提供的相互作用信息都能生效。
另外注意,以上是该文件的常用格式之一,前提是采用了矩阵形式的两体相互作用。另外也可采用标量形式的两体相互作用,此时需要在 PASP.input 中设置“ spin_lat.general_J F ”和“ spin_lat.LJmatSym F ”,这时,第一部分数据的“每行内容”中“J矩阵(逐行填写矩阵元,共9个数)”简化为“J值(仅1个数)”,其他部分内容都不变。前面的例子在该情形下可以相应地改成:
#=========================================#
2 #共几组相互作用 #以下三行提供unit_cell.str的晶格信息
5.0523118545661250 0.0000000000000000 0.0000000000000000
0.0000000000000000 5.0523118545661250 0.0000000000000000
0.0000000000000000 0.0000000000000000 5.0523118545661250
1 0.0 1 1 -1.79817 0.72799 1.79817 -1.79817 0.72799 1.79817 #single ion
2 -0.02858 1 1 1.79817 3.25414 0.72799 0.72799 1.79817 3.25414 #J1
0 # no dJ/du, i.e., no spin-lattice interaction
0 # single site anisotropy
0 # DM
2 #共几组四阶点乘形式相互作用
1 1 -0.005885 1 1
1.79817 3.25414 0.72799 0.72799 1.79817 3.25414
2 2 0.002435 1 1
1.79817 3.25414 0.72799 -0.72799 -0.72799 -0.72799 3.25414 0.72799 1.79817
#=========================================#
3.4 输入文件distortion.pos¶
“Model Invariant”中(参见2.2.1节),当“ Invariant.cal_para ”取T且“ local_mode.cal_para_method ”设置值为6(参见3.1.7.7节)时,可利用 distortion.pos (和 distortion.MAGMOM )文件生成自定义的构型。
其中 distortion.pos 文件与POSCAR格式(VASP的输入文件之一)基本一致,需要给定超胞的原子坐标信息。该文件兼容以下两种格式:A.第一行提供任意内容,第五行提供各元素符号,第六行提供各元素的原子个数(参见3.1.3.8节格式A示例文件 POSCAR );B.第一行提供各元素符号,第五行直接提供各元素的原子个数(参见3.1.3.8节格式B示例文件 POSCAR )。
格式A示例文件(以2×2×2超胞的 \(TbMnO_{3}\) 为例):
#=========================================#
TbMnO3
1.0000000000000000
10.586290000000 0.000000000000 0.000000000000
0.000000000000 11.676820000000 0.000000000000
0.000000000000 0.000000000000 14.805020000000
Tb Mn O
32 32 96
Direct
0.491570000000 0.041215000000 0.125000000000
0.491570000000 0.041215000000 0.625000000000
0.491570000000 0.541215000000 0.125000000000
……中间省略若干行
0.601970000000 0.586885000000 0.775510000000
#=========================================#
格式B示例文件(以2×2×2超胞的 \(TbMnO_{3}\) 为例,完整版可在 “example_public/Magnetic_noSOC_TbMnO3/input” 文件夹下找到):
#=========================================#
Tb Mn O
1.0000000000000000
10.586290000000 0.000000000000 0.000000000000
0.000000000000 11.676820000000 0.000000000000
0.000000000000 0.000000000000 14.805020000000
32 32 96
Direct
0.491570000000 0.041215000000 0.125000000000
0.491570000000 0.041215000000 0.625000000000
0.491570000000 0.541215000000 0.125000000000
……中间省略若干行
0.601970000000 0.586885000000 0.775510000000
#=========================================#
先介绍格式A:第一行提供任意内容(常用于标注体系信息);第二行写后续数据的整体放大倍数(scaling factor);第三至五行分别提供三个基矢的x、y、z(笛卡尔坐标)分量;第六行需要写各元素的化学符号;第七行写各元素个数。第八行选择后续坐标的填写格式,可选笛卡尔坐标形式(首字母为C、c、K或k)或分数坐标形式(默认情形,习惯上写成“Direct”)。第九行及之后的内容为各个原子坐标,依次提供各元素的(超胞内)所有原子坐标。
格式B:第一行写各元素的化学符号(之间用若干空格隔开);第二行写后续数据的整体放大倍数(scaling factor);第三至五行分别提供三个基矢的x、y、z(笛卡尔坐标)分量;第六行写各元素个数。第七行选择后续坐标的填写格式。第九行及之后依次提供各元素的(超胞内)所有原子坐标。
3.5 输入文件distortion.MAGMOM¶
“Model Invariant”中(参见2.2.1节),当“ Invariant.cal_para ”取T且“ local_mode.cal_para_method ”设置值为6(参见3.1.7.7节)时,可利用 distortion.pos 和 distortion.MAGMOM 文件生成自定义的构型。其中 distortion.MAGMOM 文件仅在涉及自旋模式时需要提供。本文件需要逐行给出超胞中各个原子的磁矩的x、y、z分量,每行对应一个原子,顺序应当与 distortion.pos 中原子顺序一致;每行提供三个数据,依次是该原子的磁矩的x、y、z分量(非磁性原子三个数都填0)。
对于非零的自旋模式,所填写数据的模长并不重要,因为在PASP软件内部会归一化处理。这里仍以2×2×2超胞的 \(TbMnO_{3}\) 为例,示例文件如下(完整版可在 “example_public/Magnetic_noSOC_TbMnO3/input” 文件夹下找到):
#=========================================#
0 0 0
0 0 0
……(共计连续32行“0 0 0”)
0 0 0
-1.9464 -2.8302 2.0498
2.6410 2.0453 -2.2005
……(共计连续32行非零随机向量)
-2.5616 -1.0720 -2.8791
0 0 0
0 0 0
……(共计连续96行“0 0 0”)
0 0 0
#=========================================#
3.6 输入/输出文件local_mode_PM.dat¶
在“Model atomic_effective_H”中,为了避免反复重新分析不等价相互作用,通常会先用“Model Invariant”执行一次不等价相互作用分析(参见2.2.1节),获得 local_mode_PM.dat 输出文件,再将该文件作为后续MC、MD等模拟分析的输入文件。有时也会反复利用此文件执行“Model Invariant”,分别处理不同构型,获取后续步骤所需的 *.ene_symbol 文件。
本文件通常不需要手动修改,用程序自身生成即可。需要将已有的 local_mode_PM.dat 文件作为输入文件时,注意在 PASP.input 中设置“ local_mode.read_interaction T ”。
3.7 输入文件J_best.dat¶
在“Model atomic_effective_H”中用该文件提供相互作用参数的取值信息。
注意:该文件采用严格的逐行读取规则,不能任意空行。
示例文件如下(#后面的内容为注释部分,无需写出;注意这里#号需要用空格或制表符与数据隔开;此外#号开头的首尾两行不算在文件内容之内):
287 4 #不等价相互作用数(与*.ene_symbol中的个数一致);保留参数个数
1 0.1772080263938097E-02 #保留原1号参数;1号参数值
3 -0.8077197635063232E-02 #保留原3号参数;3号参数值
5 0.1859024576895017E-02
15 0.1540675214074116E-02
第一行提供两个数据:不等价相互作用分析给出的总相互作用数,可在名为 *.ene_symbol (第一行数据)或 all_interaction_type_Spin_xyzform.dat (最后一行的第一个数据)的输出文件中查得;第二个数据是MC等模拟中采用的相互作用参数个数(不计常数项)。
后面逐行提供各相互作用参数的信息:先提供参数编号(与不等价相互作用分析所得的输出文件 all_interaction_type_Spin_xyzform.dat 或 local_mode_PM.dat 中的编号一致),再提供相互作用值。注意这里假定自旋矢量归一化,无量纲;因此相互作用量纲与能量量纲一致,取eV单位。
3.8 输入文件Fitting_settings.txt¶
在“Model Fitting_one_order”中(MLMCH方法确定哈密顿量参数,参见2.2.2节),需要用到该输入文件。注意在该文件中,仅在每行读取开头的数据(除了在第三行需要读取4个数据外),而后面的文字部分仅用于注释;该文件是逐行读取相应设置内容的,不允许任意调换两行顺序或增减行数等。
以下示例文件中的 Fitting_Settings.txt 全部采用的是缺省设置,缺省该文件时即按缺省设置决定各设置项。后面将逐行介绍各设置项含义(本文件中涉及是否的设置项,用1或其他非零整数表示是,0表示否)。#号开头的首尾两行不算在文件内容之内。注释信息中的感叹号或双感叹号用于标记设置项的重要程度。
#=========================================#
1 I_Read_Settings: 1
0 I_CONVERT_TO_ONE_ORDER: 0
30 0 30 1 N_UPBOUND_TOTAL,N_UPBOUND_X,N_UPBOUND_THETA,COMBINE_TYPE
1 I_GIVE_PREDICT: Usually 1.
0 !! I_ONLY_PREDICT: Usually 0. Use 1 when finally giving reports(with I_AUTOINIT=5).
0 !! I_CHECK_SELFPREDICT: Try 0 and 1. Usually 0 is better (but not always).
0.500E+00 !! MAX_Nncheck_BY_Nn: Usually 0.5 (Not important if I_CHECK_SELFPREDICT=0).
0 ! I_SET_TERM_VALUE: Usually 0. When 1, use Fitting_Set_Term_Value.txt
0 ! I_HAVE_KEEP_TERM: Usually 0. When 1, use Fitting_Set_Term_Keep.txt
0 ! I_HAVE_SKIP_TERM: Usually 0. When 1, use Fitting_Set_Term_Skip.txt
0 ! I_CHANGE_WEIGHT: Usually 0(Do not set);1(set by Fitting_Weight.txt);2(set by BETA_WEIGHT).
0 ! I_CHECK_SAMEDATA: Usually 0. If 1, delete the redundant row of data (DONNOT USE 1 WHEN I_SET_TERM_VALUE==1 or I_SET_TERM_DEPENDENT==1).
1 ! I_CHECK_DATA: Usually 1. (Sometimes 0 when dealing with the already checked data)
0.100E-07 ! CHECK_DATA_ACCURACY: Usually 0 or 1e-8. If Relative Error<=CHECK_DATA_ACCURACY, data are regarded as the same.
0 !! I_RANDOM_CHANGE_DATA: Use 0 First. If errors occur, use 1 or block some parameters or try a LARGER CHECK_DATA_ACCURACY.
1 !! I_AUTOINIT: 1:Only constant term! 5: User-defined!(Use Fitting_Set_Init.txt) 2:Initially try each parameter to determine initial form.
1 !! SEARCH_TYPE: 1:My(Usually)! 2:add(complete)&delete. 3:only add(complete). 4:My(complete when adding). 5:My(Accurate add). 6:My(Accurate del)
1 BetterType: 1 (Or 2, with different settings of lambdas, not recommended).
1 ! BetterType_subs1: 1 (or 2).
1 ! BetterType_check_del: 1 (or 2).
1 ! BetterType_check_add: 1 (or 2).
1 BetterType_check_subs1: 1
0 ! I_TRY_SUBSTITUTE2: Usually 0 (or 1). If 0, only use 1 for the 'BetterTypes' below.
1 ! BetterType_subs2: 1 (or 2).
1 ! BetterType_check_subs2a: 1 (or 2).
1 ! BetterType_check_subs2b: 1 (or 2).
0 ! I_SET_TERM_DEPENDENT: Usually 0. When 1, use Fitting_Set_Term_Dependent.txt
0 ! SHOW_STDOUT: Usually 1(show more information but slower). Maybe 0 is better when using Lattice_model.
0.50000E+02 ! BETA_WEIGHT(Bw): IF I_CHANGE_WEIGHT=2,then weight proportional to exp(-Bw*E). E(eV)->Bw=11588.74/T(K).
#=========================================#
I_Read_Settings: 是否读取 Fitting_Settings.txt 文件信息。
I_CONVERT_TO_ONE_ORDER: 是否先对各个自变量执行某种展开方式(支持泰勒展开、傅里叶展开等),再对展开所得的中间变量进行筛选参数及拟合步骤。由于通常利用“Model Invariant”分析得到中间变量,作为本文件的自变量,通常不需要在该步骤中再作任何展开处理。
N_UPBOUND_TOTAL,N_UPBOUND_X,N_UPBOUND_THETA,COMBINE_TYPE: 这四项在同一行设置,本行仅在前一行非零时生效。用于设定对自变量展开的方式和阶数。N_UPBOUND_TOTAL为总的最大阶数,N_UPBOUND_X为坐标类型变量(采用泰勒展开)的最大展开阶数,N_UPBOUND_THETA为角度类型变量(采用傅里叶或球谐函数展开)的最大展开阶数,COMBINE_TYPE本意用于选择函数形式(暂不起任何作用)。各个自变量看作坐标还是角度类型,以及对于角度类型变量如何处理,目前仅限于在代码内部修改设定,暂未支持利用外部文件设置。因此本行设置内容目前仅用于内部测试,对用户而言不起作用。
I_GIVE_PREDICT: 是否使用测试集数据。通常总是建议取1。
I_ONLY_PREDICT: 是否直接使用初始模型,进行SBS搜索步骤(参见2.2.2节的图2.2.3)。选1时会跳过搜索最优模型的环节,常用于针对已有的最优模型(作为初始模型),给出各参数重要性排序。
I_CHECK_SELFPREDICT: 是否从训练集数据( Fitting_Dataset.txt 文件)中分出一部分来作为验证集。选1时使用验证集;选0时不使用验证集。
MAX_Nncheck_BY_Nn: 使用验证集时,验证集占 Fitting_Dataset.txt 文件中数据量的比例。
I_SET_TERM_VALUE: 是否设定部分参数的取值(由 Fitting_Set_Term_Value.txt 文件设定,参见2.2.2.8节)。
I_HAVE_KEEP_TERM: 是否设定强制保留部分参数(由 Fitting_Set_Term_Keep.txt 文件设定,参见2.2.2.6节)。
I_HAVE_SKIP_TERM: 是否设定强制跳过部分参数(由 Fitting_Set_Term_Skip.txt 文件设定,参见2.2.2.7节)。
I_CHANGE_WEIGHT: 是否修改各数据的权重。0为默认情形,所有数据取相同权重;1是用 Fitting_Weight.txt 提供各数据权重(每行提供一个权重数据,训练集在前,测试集在后,依次写出各个数据的权重);2是根据后面 BETA_WEIGHT(Bw) 设置项,按正比于exp(-Bw*E)的方式设定各数据权重,其中能量E即训练集和测试集最后一列的数据(通常为能量,单位为eV)。
I_CHECK_SAMEDATA: 是否检测重复数据行。取1时,检测并删除多余的重复数据行。注意在I_SET_TERM_VALUE或I_SET_TERM_DEPENDENT非零时,本项需要取0。
I_CHECK_DATA: 是否检测并删除明显的冗余数据列,主要涉及取值为常数的列,或者完全成正比例的两列。取1时,检测并删除明显的冗余数据列。注意在I_SET_TERM_VALUE或I_SET_TERM_DEPENDENT非零时,本项需要取0。
CHECK_DATA_ACCURACY: 前一项设置非零时(检测并删除明显的冗余数据列),本项设置两项数据的相对误差小于多少时视为相等。
I_RANDOM_CHANGE_DATA: 是否随机对所有数据产生微扰。本意是用于避免出现不可逆情形,但该处理方式效果不好,现已不常用。建议总是取0。
I_AUTOINIT: 控制初始模型的设定方式。选1表示初始只保留常数项;选2表示初始不含任何项(不推荐);选5表示自定义初始模型(由 Fitting_Set_Init.txt 文件设定,参见2.2.2.4文件)。
SEARCH_TYPE: 搜索最优模型的算法。选1表示主要推荐使用的MLMCH方法(参见2.2.2节);选2表示仅考虑加项、删项(不考虑替换项)的搜索方法,每轮加项搜索都是完整尝试各种可能性后选择拟合效果最优的方式;选3表示仅考虑加项的搜索方法,每轮加项搜索都是完整尝试各种可能性后选择拟合效果最优的方式(即SFS算法); 选4表示考虑加项、删项、替换项的搜索方法,每轮加项搜索都是完整尝试各种可能性后选择拟合效果最优的方式。现仅1和3常用,其他选项不推荐。
BetterType、BetterType_subs1、BetterType_check_del、BetterType_check_add、BetterType_check_subs1、I_TRY_SUBSTITUTE2、BetterType_subs2、BetterType_check_subs2a、BetterType_check_subs2b: 这些都是涉及MLMCH方法(参见2.2.2节)内部的算法逻辑细节的设置选项,强烈建议取默认值,不必尝试其他选项。这些设置项是为了测试不同算法逻辑的效果优劣而添加的选项,最后保留了效果最好的设置方式。
I_SET_TERM_DEPENDENT: 是否设定部分参数的线性约束关系(由 Fitting_Set_Term_Dependent.txt 文件设定,参见2.2.2.9节)。
SHOW_STDOUT: 是否在标准输出中提供搜索过程的细节。由于输出搜索细节会严重拖慢速度,一般强烈建议取0。
BETA_WEIGHT(Bw): 参见前述设置项 I_CHANGE_WEIGHT 的相关内容。
另外注意,在运行PASP后,会自动生成输出文件 Fitting_Settings_Save.txt ,它是按 Fitting_Settings.txt 格式写的,各设置项内容是运行PASP时它们的实际取值。如果一开始是缺省该文件运行的,可以如此获取填写了默认内容的示例文件。
3.9 输入文件Fitting_Set_Lambda.txt¶
在“Model Fitting_one_order”中(MLMCH方法确定哈密顿量参数,参见2.2.2节),可能需要用到该输入文件。示例文件如下:
#=========================================#
20 1 N_LAMBDA,I_LAMBDA
1 158 0.1299999952E+01 I,Nc_p_s(I),LAMBDAS(I)
2 158 0.1200000048E+01 I,Nc_p_s(I),LAMBDAS(I)
3 158 0.1100000024E+01 I,Nc_p_s(I),LAMBDAS(I)
4 158 0.1080000043E+01 I,Nc_p_s(I),LAMBDAS(I)
5 158 0.1059999943E+01 I,Nc_p_s(I),LAMBDAS(I)
6 158 0.1039999962E+01 I,Nc_p_s(I),LAMBDAS(I)
7 158 0.1029999971E+01 I,Nc_p_s(I),LAMBDAS(I)
8 158 0.1019999981E+01 I,Nc_p_s(I),LAMBDAS(I)
9 158 0.1014999986E+01 I,Nc_p_s(I),LAMBDAS(I)
10 158 0.1009999990E+01 I,Nc_p_s(I),LAMBDAS(I)
11 158 0.1008000016E+01 I,Nc_p_s(I),LAMBDAS(I)
12 158 0.1006000042E+01 I,Nc_p_s(I),LAMBDAS(I)
13 158 0.1004999995E+01 I,Nc_p_s(I),LAMBDAS(I)
14 158 0.1003999949E+01 I,Nc_p_s(I),LAMBDAS(I)
15 158 0.1003000021E+01 I,Nc_p_s(I),LAMBDAS(I)
16 158 0.1001999974E+01 I,Nc_p_s(I),LAMBDAS(I)
17 158 0.1001500010E+01 I,Nc_p_s(I),LAMBDAS(I)
18 158 0.1001000047E+01 I,Nc_p_s(I),LAMBDAS(I)
19 158 0.1000499964E+01 I,Nc_p_s(I),LAMBDAS(I)
20 158 0.1000000000E+01 I,Nc_p_s(I),LAMBDAS(I)
#=========================================#
示例文件全部采用的是缺省设置,换言之,只需要默认版本的MLMCH方法时,可以省略该输入文件。该输入文件中第一行提供两个数据,分别表示后续提供几行数据(通常每行数据对应一个新的λ值,对应一轮大的搜索循环),以及从其中第几行开始使用。后面每行有三个有效数据,分别是第几行数据、本轮循环中允许模型中包含的最大参数个数、本轮循环中采用的λ值。这里的示例文件中共提供20行数据,对应20个递减的λ值,其中最后一个λ值恰好为1.0。注意λ值取1.0的最后一轮循环可能会显著偏慢,如果希望节省搜索时间,可以考虑把第一行的第一个数据由20修改为19或者更小,从而回避λ值取1.0的较慢的搜索过程。
另外注意,在运行PASP后,会自动生成输出文件 Fitting_Set_Lambda_Save.txt ,它是按 Fitting_Set_Lambda.txt 格式写的,各设置项内容是运行PASP时它们的实际取值。如果一开始是缺省该文件运行的,可以如此获取填写了默认内容的示例文件。
3.10 输入文件spin3.in¶
在“Model Spin_lattice_interaction”中,“ Read_init_spin ”取T时,从 spin3.in 中读取初始自旋构型。在“Model KNB”中,也需要用 spin3.in 指定自旋构型(无需设置“ Read_init_spin ”项)。另外,在“Model find_J_path_sym”中,也可使用 spin3.in 指定参考构型(无需设置“ Read_init_spin ”项),在四态法中将在参考构型的基础上适当调整部分原子的自旋取向,用于进行若干组第一性原理计算。
文件格式示例如下:
#=========================================#
1 -0.54157046 -0.56570479 -0.62183562 #原子编号;归一化的自旋矢量
2 -0.54499053 -0.56493211 -0.61954582
3 -0.54407759 -0.56227264 -0.62275923
4 -0.54356094 -0.56410803 -0.62154938
5 0.00000000 0.00000000 0.00000000 #非磁性原子提供零向量
6 0.00000000 0.00000000 0.00000000
7 0.00000000 0.00000000 0.00000000
8 0.00000000 0.00000000 0.00000000
9 -0.54157997 -0.56568915 -0.62184155
……
508 -0.54355896 -0.56411667 -0.62154327
509 0.00000000 0.00000000 0.00000000
510 0.00000000 0.00000000 0.00000000
511 0.00000000 0.00000000 0.00000000
512 0.00000000 0.00000000 0.00000000
#=========================================#
该文件需要依次提供超胞中各个原子的编号和自旋矢量(归一化或零)的三个分量。原子顺序必须与基于 cell.str 结构、经“ block SuperCell ”扩胞所得超胞中原子的编号顺序一致。由于“ block SuperCell ”扩胞所得原子顺序难以事先预计,通常在使用 spin3.in 时,建议不通过“ block SuperCell ”扩胞,而直接在 cell.str 中提供超胞结构信息。这样 spin3.in 原子顺序只需要与 cell.str 中原子顺序一致即可。
3.11 输入文件amp_local_mode.in¶
在“Model atomic_effective_H”中,“ Read_init_spin ”取T时,从 amp_local_mode.in 中读取初始构型(各个局域模式的大小以及各个strain模式的大小)。
该文件格式与“Model atomic_effective_H”运行MC时的输出文件 lowest_ene.amp_local_mode 一致(见2.2.3节),需要依次给出初态的各个局域模式以及应变的大小,示例如下:
#=========================================#
1 2.901785753659 -4.162823203431 3.369777246670 #第1个有局域模式的原子;该原子各局域模式的大小
2 3.186716707285 -4.515955600339 3.587299249456
3 4.424829790741 3.383234868544 4.547196266060
……
512 3.469348208439 -3.276650367835 -3.992938680425
0.000000000000 0.000000000000 0.000000000000 0.000000000000 0.000000000000 0.000000000000 #strain
#=========================================#
编号与原子坐标的对应关系,以及每个原子具有的局域模式数,可在“Model atomic_effective_H”运行MC时的输出文件 lowest_ene.str_mode_amp 文件中查得(见2.2.3节。如果一开始缺少该文件,可以先不设置初始构型,用很少的步数完成一次MC模拟,以获得该输出文件)。
另外注意,在“Model Invariant”分析指定构型或随机构型的 *.ene_symbol 文件时,也会同时产生相应的 *.amp_local_mode 文件,这种文件与此处需要的 amp_local_mode.in 文件格式是一致的,可以直接拿来使用(重命名即可)。
3.12 输入文件Zeff.dat¶
在使用“Model Spin_lattice_interaction”计算自旋序诱导铁电极化时,可能用到此输入文件,用于提供Born有效电荷数据。完整示例文件参见 “example_public/P_by_spin_order/ion_strain/input/Zeff.dat” ,以下提供部分内容示例(含注释):
#=========================================#
BORN EFFECTIVE CHARGES (in e, cummulative output) #任意内容
------------------------------------------------- #任意内容
ion 1 #离子编号:格式“空格ion空格I4(读取四位的整数)”
1 4.88158 -0.18395 -0.00008 #dF/dEx的三个分量(读取格式I5,3F12.5)
2 0.18406 4.88147 -0.00003 #dF/dEy的三个分量(读取格式I5,3F12.5)
3 0.00000 0.00000 4.32870 #dF/dEz的三个分量(读取格式I5,3F12.5)
ion 2
1 4.88158 0.18395 -0.00008
2 -0.18403 4.88148 0.00009
3 0.00000 0.00000 4.32870
……(省略若干行)
ion 10
1 -2.87183 0.53177 -0.44983
2 0.29963 -3.10349 -0.45424
3 -0.42638 -0.57577 -2.63409
#=========================================#
注意读取的时候是严格按字符数读取的,如I5连读五个字符,F12.5连读12个字符。
该文件内容通常是从VASP计算(DFPT功能)所得OUTCAR中截取的。
3.13 输入文件elastic.dat¶
在使用“Model Spin_lattice_interaction”计算自旋序诱导铁电极化时,可能用到此输入文件,用于提供应变张量信息、弹性常数、压电张量等信息。完整示例文件参见 “example_public/P_by_spin_order/ion_strain/input/elastic.dat” ,以下提供部分内容示例(含注释):
#=========================================#
10 #原胞中原子个数
#INTERNAL STRAIN TENSORS FROM STRAINED CELLS (eV/Angst)
-1.93347 1.92110 -0.00000 2.08596 1.06465 2.21452
……(省略若干行内容)
-3.17730 -3.02813 -3.95397 2.59235 0.56302 -2.41944
#ion-clamped elastic constant (kBar)
3220.8864 1498.2284 1222.7964 0.0000 0.0000 -109.5768
1498.2284 3220.8864 1222.7964 0.0000 0.0000 109.5768
1222.7964 1222.7964 2950.5556 0.0000 0.0000 -0.0000
-0.0000 0.0000 0.0000 861.3290 109.5768 0.0000
-0.0000 0.0000 0.0000 109.5768 893.9731 0.0000
-109.5768 109.5768 -0.0000 0.0000 0.0000 893.9731
#ion-clamped piezoelectric tensor (e Angst)
0.92044 -0.92089 -0.00046 0.00000 0.00000 -1.62125
-0.00015 0.00033 0.00006 -0.92087 -1.62239 -0.00040
1.12739 1.12739 -4.12861 -0.00000 0.00000 0.00000
#=========================================#
该文件第一行需手动填写,剩余内容通常是从VASP计算(DFPT功能)所得OUTCAR中截取的。
3.14 输入文件spin_strain.dat¶
在使用“Model Spin_lattice_interaction”计算自旋序诱导铁电极化时,可能用到此输入文件,用于提供海森堡相互作用参数J对应变的导数。示例文件如下:
#=========================================#
1 #以下读取几行数据
1 -0.0460396 -0.0951899 -0.0871019 -0.0761737 0.0272722 0.0321033 #d_J/d_eta
#=========================================#
该文件第一行指出后续读取几行数据。之后每行数据内容包括:第几个相互作用J(对应 spin_exchange.dat 中第一部分内容信息),该J值对六个应变自由度的导数(单位eV)。
3.15 输入文件DM_derivative.dat¶
在使用“Model Spin_lattice_interaction”计算自旋序诱导铁电极化时,可能用到此输入文件,用于提供DM相互作用参数对离子位移的导数。完整示例文件参见 “example_public/P_by_spin_order/ion_strain/input/DM_derivative.dat” ,以下提供部分内容示例(含注释):
#=========================================#
1 #共几组数据
1 1 #第1组数据;第1种DM相互作用
-6.441774129000 11.157480082400 9.245866623200
-3.220887064500 -5.578740041200 4.622933311600
6.441774128900 0.000000000000 4.622933311600
80
0.000000000000 0.000000000000 0.000000000000
-3.220887064500 5.578740041200 4.622933311600
……(省略若干行)
-0.000020250000 0.000020750000 0.000018500000
#=========================================#
该文件第一行指出后续读取几组数据。之后每组数据中:先给出这是第几组数据,对应第几种DM相互作用(对应 spin_exchange.dat 中第四部分内容信息);
该部分内容示例如下。第一行提供一个整数,表示后续有几组数据(每组数据对应一种DM相互作用对各个原子位移偏导的信息)。之后每组信息按如下格式填写:第几组数据、对应第几种DM相互作用(编号与 spin_exchange.dat 中第四部分定义顺序一致);之后的3×3矩阵提供扩胞后的基矢(单位Ang);其后一行提供一个数字,表示对于当前DM相互作用,提供对于多少原子位置的偏导信息,例如80个原子(通常等于扩胞后胞内原子数);之后提供这80个原子的坐标(笛卡尔坐标系,单位Ang,共80行,每行3个数),再依次给出该DM相互作用的x分量对于各个原子坐标分量的偏导(eV/Ang,共80行,每行3个数),空一行后,依次给出该DM相互作用的y分量对于各个原子坐标分量的偏导(eV/Ang,共80行,每行3个数),再空一行后,依次给出该DM相互作用的z分量对于各个原子坐标分量的偏导(eV/Ang,共80行,每行3个数)。
3.16 输出文件PASP.used_info¶
本输出文件提供了PASP运行时,相关的各设置项(其中有些输出的设置项其实与当前使用的功能无关)的实际取值。恰好采用默认值的设置项,会在相应取值信息后标注“ # Default value ”。部分内容示例如下:
#=========================================#
#FDF: Opened PASP.input for input. Unit: 11
fdf-debug 0 # Default value
Model Fitting_one_order
DFT.home_made T # Default value
SpinW_Toch F # Default value
printlevel 1 # Default value
external_prog VASP # Default value
system.dimension 3 # Default value
write_info 1 # Default value
MC.measure 50 # Default value
number_of_species 1
LatticeConstant 1.889725989 Bohr
# Above item originally: LatticeConstant 1.000000000 Ang
……(中间省略若干行)
Rad.Max_scale 2.000000000 # Default value
Rad.Min_scale 0.7000000000 # Default value
#=========================================#
- 18
MIYATAKE Y, YAMAMOTO M, KIM J J, et al. On the implementation of the heat bath algorithms for monte-carlo simulations of classical heisenberg spin systems [J]. Journal of Physics C-Solid State Physics, 1986, 19(14): 2539-2546.