4 实例¶
4.1 BiFeO 3 结构搜索、海森堡模型及MC模拟¶
4.1.1 全局结构搜索¶
\(BiFeO_{3}\) 体系空间群为R3c,基态为G型反铁磁。我们先采用微扰空间群方法(结合遗传算法)搜索它的低能结构。该步骤的全部输入文件在 “example_public/BiFeO3/1.GA/input” 文件夹下。相关的介绍说明和注意事项见2.3节。主要输出文件 Saved_*.POS 在 “example_public/BiFeO3/1.GA/output” 文件夹下。
之后可以对上述 Saved_*.POS 进一步优化,主要是利用VASP基于各结构作弛豫优化计算,该步骤的全部输入文件在 “example_public/BiFeO3/2.opt/input” 文件夹下。先调用 opt.sh 脚本(命令行输入“ sh opt.sh ”)完成所需的VASP计算,然后再调用 E.sh 脚本获得优化后各结构的能量信息(命令行输入“ sh E.sh >E_opt.dat ”,在标准输出重定向所得文件 E_opt.dat 中即可查看)。选出其中能量最低的结构,按R3c空间群对称性将其对称化(这步可以借助FindSym等软件完成),再次用VASP弛豫优化,所得结构文件参见 “example_public/BiFeO3/2.opt/output/CONTCAR” 。
初始的高对称性结构( \(Pm\bar{3}m\) )以及优化所得R3c空间群的结构(即最后的CONTCAR结构)示意图如图4.1.1所示。

图4.1.1 \(BiFeO_{3}\) 结构示意图(磁态取G-AFM态)。(a) 初始高对称性结构( \(Pm\bar{3}m\) )的晶胞(三个基矢彼此垂直,a、b相等),体积为原胞的二倍。(b) 初始高对称性结构( \(Pm\bar{3}m\) )的原胞(三个基矢彼此夹角相等,三轴等长),原胞各顶点的Bi原子处三个细箭头表示晶胞基矢方向。(c) 优化所得结构(R3c)的二倍胞(三个基矢近似彼此垂直,a、b近似相等),它不是晶胞,但可用于与图(a)对比。(d) 优化所得结构(R3c)的原胞(三个基矢彼此夹角相等,三轴等长),原胞各顶点的Bi原子处三个细箭头表示二倍胞基矢方向。¶
4.1.2 四态法计算海森堡模型参数¶
为了针对上步所得结构文件 CONTCAR ,构造磁相互作用模型。我们在示例中采用最简单的海森堡模型,保留前三近邻相互作用,并采用四态法来计算。
MAGMOM 设置,在 run_DFT.sh 脚本中再给 INPUT 文件补充相应设置项)、 KPOINTS 、 POSCAR 、 POTCAR 文件,提交VASP任务所需的 vasp.slurm 文件,运行 run_DFT.sh 脚本即可(根据具体情况可能要适当修改脚本内容)。cal_spin_exchange T ”,这样可自动根据J%d(%d为数字1、2等)文件夹内 upup 、 updn 、 dnup 、 dndn 四个文件夹内的VASP计算结果计算得到各向同性的J值并编辑生成相应的 spin_exchange.dat 文件(目前此功能仅支持各向同性的J值,对于更复杂的情形,仍需自己编写脚本生成 spin_exchange.dat 文件或手动输入,格式参见3.3节,四态法计算公式参见2.1.2.1节)。将这些输入文件放在上一步运行 run_DFT.sh 的路径下,运行PASP即可得到后续步骤所需的 spin_exchange.dat 文件。4.1.3 蒙特卡洛模拟¶
本例采用“ Model Spin_lattice_interaction ”进行PTMC模拟(参见2.1.3节),该步骤的全部输入文件在 “example_public/BiFeO3/4.PTMC/input” 文件夹下。其中 spin_exchange.dat 文件是上一步的输出文件,这里是保留了前三近邻的各向同性海森堡相互作用。部分重要输出文件在 “example_public/BiFeO3/4.PTMC/output” 文件夹下,其中 lowest_onlyspin.xsf 给出PTMC中的最低能量态信息,近似为G-AFM态(如果后续进行CG局域优化,可以得到更严格的G-AFM态); C_PTMC_K.dat 给出热容随温度变化,根据热容取极大值时的温度,可判断相变温度约480K。
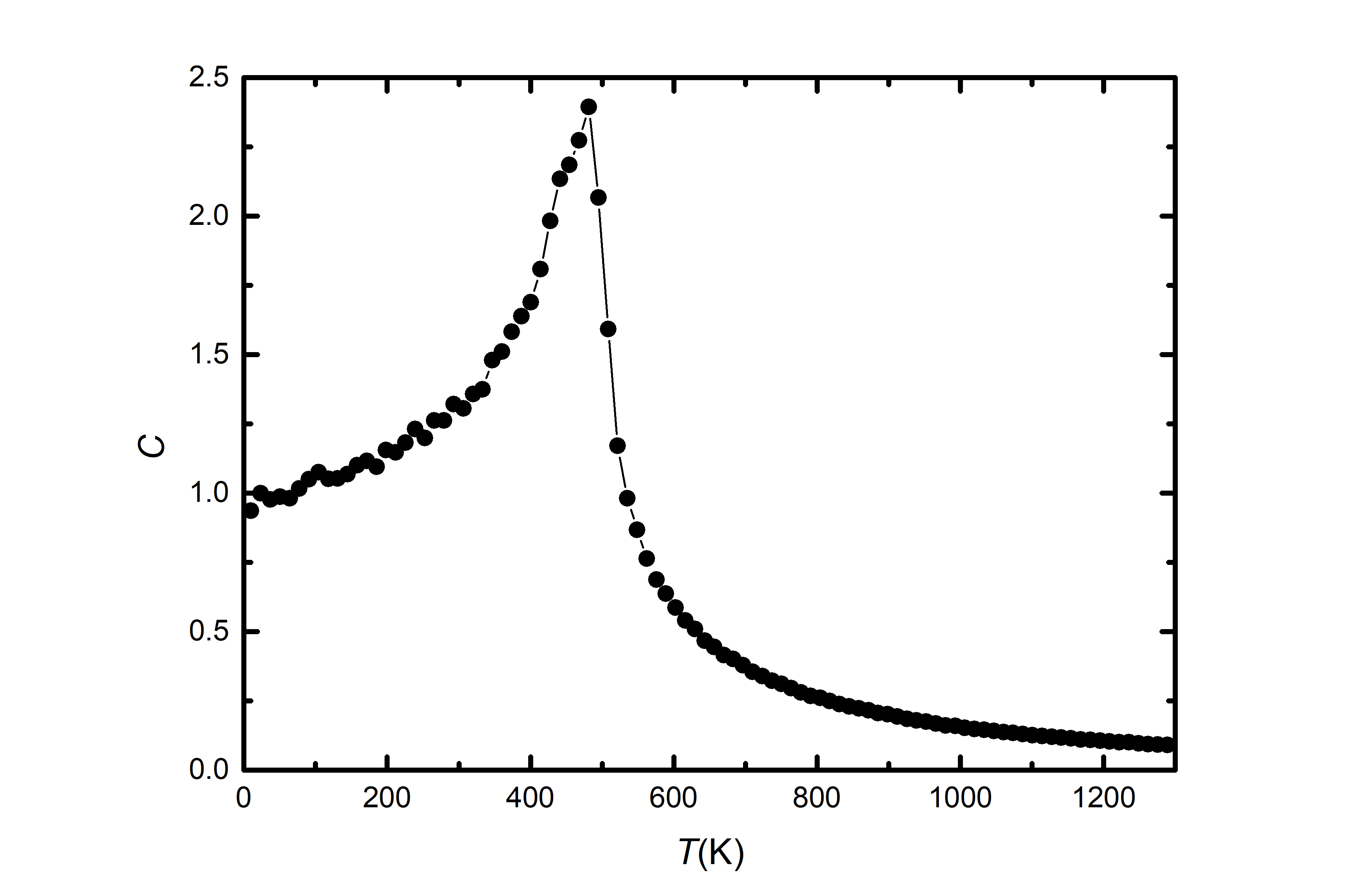
图4.1.2 PTMC模拟所得 \(BiFeO_{3}\) 热容随温度变化图¶
4.2 单层NiCl 2 有效自旋哈密顿量构造及蒙特卡洛模拟¶
4.2.1 随机产生磁构型并分析不等价相互作用贡献¶
首先准备优化之后的原胞的 POSCAR 文件(优化步骤通过VASP完成,这步的细节已省略)。为了准备5×4×1超胞,参见3.1.3.8节内容,使用post_VASP得到扩胞后的 POSCAR.multi 文件。这步示例输入输出文件在 “example_public/NiCl2/0.sc541” 文件夹下。将输出文件 POSCAR.multi 重命名为POSCAR供下步使用,将扩胞前的原胞结构 POSCAR 文件重命名为 POSCAR_UC 供下步使用。
接下来利用PASP产生200个随机的磁构型(每个磁性原子的自旋随机取向),并分析相应的 \(\left\{h_{j}^{(i)}\right\}\) 值(定义见2.2.1节或2.2.2节),得到相应的 *.ene_symbol 文件(用于输出 \(\left\{h_{j}^{(i)}\right\}\) 值信息)。这步的输入文件在 “example_public/NiCl2/1.Invariant_200structures/input” 文件夹下,这里采用了3.1.3.7节和3.1.4.4节的技巧,直接用 POSCAR 和 POSCAR_UC 文件代替了 cell.str 和 unit_cell.str 文件。主要输出文件在 “example_public/NiCl2/1.Invariant_200structures/output” 文件夹下,总共会产生200组随机构型的 *.ene_symbol 文件和 *.vasp_MAGMOM 文件(示例文件中省略)。
4.2.2 VASP计算各构型的能量¶
对于上一步随机产生的磁构型,我们需要用VASP(或其他第一性原理计算软件)计算它们各自的能量。为此,我们要先批量准备 INCAR 文件,每个 INCAR 文件包含相应的 MAGMOM 和 M_CONSTRstr 设置信息。这步的输入文件在 “example_public/NiCl2/2.VASP/input1” 文件夹下(另外还有若干 *.vasp_MAGMOM 文件),其中 INCAR 文件提供VASP计算的主要设置信息(但不包含 MAGMOM 和 M_CONSTRstr 设置项内容;在本示例中为了方便测试,降低了VASP计算精度), createINCAR.sh 脚本用于从 *.vasp_MAGMOM (上一步的输出文件)读取磁矩信息,写入 INCAR_all 文件夹下各个INCAR_*的 MAGMOM 和 M_CONSTRstr 设置项中。运行 createINCAR.sh 脚本所得( INCAR_all 文件夹下) INCAR_* 文件是在 INCAR 文件内容后面追加了 MAGMOM 和 M_CONSTRstr 设置项的文件。为了额外生成参考态(取铁磁态)的 INCAR 文件,事先准备好 0.vasp_MAGMOM 文件(模仿其他 *.vasp_MAGMOM 文件,按铁磁态填写磁矩信息即可),这样输出文件会增加INCAR_all/INCAR_0。
接下来,除了上一步所得 INCAR_all 文件夹外,还需另外准备的其他输入文件在 “example_public/NiCl2/2.VASP/input2” 文件夹下,这里 KPOINTS 文件也采用较低的精度(为了方便快速测试),先运行 create_vasp_inputs.sh 脚本生成各个第一性原理计算的文件夹(这里编号0-200,其中编号0对应参考态,这里是铁磁态),再运行 submit_vasp_jobs.sh 脚本批量提交任务(示例中是each=5个文件夹为一组,每个提交的任务依次完成5个文件夹内的VASP计算)。最后再用 getallenergy_r.sh 脚本获取所有构型的能量信息(减去参考态能量),所得输出文件为 Energy.dat 。
然后就可以准备下一步所需的训练集、测试集数据了。这里可以使用编译好的Fortran程序 convert_data (源代码文件为 convert_data.f90 ,用“mpiifort convert_data.f90 -o convert_data”命令编译,再提供执行权限即可),在 convert_info.txt 中设置训练集数目、测试集数目(因为共200组随机构型,所以训练集和测试集应当共200个)和扩胞数(第一性原理计算所用超胞包含多少个原胞)即可。所需的其他输入文件包括 ene_symbol 文件夹(里面包含4.2.1节步骤产生的所有 *.ene_symbol 文件)和 Energy.dat 文件(在上一步得到)。这步所需的全部示例输入文件在 “example_public/NiCl2/3.prepare_dataset/input” 文件夹下。这里使用的 *.ene_symbol 和 Energy.dat 文件的数据实际上是文献 19 中原始计算所得数据(采用了更高的第一性原理计算精度),而非前述步骤的示例输入文件所得数据(示例文件中为了便于测试,降低了计算精度)。输出文件在 “example_public/NiCl2/3.prepare_dataset/output” 文件夹下,分别是训练集数据 Fitting_Dataset.txt 和测试集数据 Fitting_Data_for_prediction.txt 。
4.2.3 MLMCH方法构造有效自旋哈密顿量¶
接下来采用MLMCH方法(2.2.2节)筛选重要相互作用项并拟合,构造后续MC所需的有效自旋哈密顿量。这步所需的全部示例输入文件在 “example_public/NiCl2/4.MLMCH/input” 文件夹下。其中 Fitting_Dataset.txt 和 Fitting_Data_for_prediction.txt 是上一步所得文件。再另外准备 PASP.input ,运行PASP即可。所得主要输出文件在 “example_public/NiCl2/4.MLMCH/output” 文件夹下。程序自动推荐的是使用了11个参数的模型(包含常数项),但通过观察 Report_fitting.txt 中最后几行的最后一列数据,可以发现使用4个参数(包含常数项)的模型就已经达到很高的精度,因此我们在后续MC步骤中可以仅使用3个参数(去掉了常数项,保留的3个参数依次对应文献 19 中的、和)。该模型对应 Report_fitting_function_GRAD_4_LM.txt 文件,因此可将该文件复制成 J_best.dat ,作为下一步MC的输入文件之一。
4.2.4 蒙特卡洛模拟¶
本例采用“ Model atomic_effective_H ”进行PTMC模拟(参见2.2.3节),该步骤的全部输入文件在 “example_public/NiCl2/5.MC/input” 文件夹下。其中 J_best.dat 文件是上一步所得; local_mode_PM.dat 是在4.2.1节步骤所得输出文件; pasp.slurm 仅用于提交PASP任务(这里给出提交任务的文件是为了提示注意提交任务时进程数设置, PASP.input 中PT.M必须是进程数的整数倍)。部分重要输出文件在 “example_public/NiCl2/5.MC/output” 文件夹下,其中 relax-lowest_onlyspin.xsf 给出PTMC中的最低能量态经CG局域优化后的磁态信息,为铁磁态; C_PTMC_K.dat 给出热容随温度变化,根据热容取极大值时的温度,可判断相变温度约23K。
- 16
TOTH S, LAKE B. Linear spin wave theory for single-q incommensurate magnetic structures [J]. Journal of Physics: Condensed Matter, 2015, 27(16): 166002.
- 17
COLPA J. Diagonalization of the quadratic boson hamiltonian [J]. Physica A: Statistical Mechanics and its Applications, 1978, 93(3-4): 327-353.
- 18
MIYATAKE Y, YAMAMOTO M, KIM J J, et al. On the implementation of the heat bath algorithms for monte-carlo simulations of classical heisenberg spin systems [J]. Journal of Physics C-Solid State Physics, 1986, 19(14): 2539-2546.
- 19(1,2)
NI J, LI X, AMOROSO D, et al. Giant biquadratic exchange in 2d magnets and its role in stabilizing ferromagnetism of nicl 2 monolayers [J]. Physical Review Letters, 2021, 127(24): 247204.