刘文剑团队三十年力作|鸿之微BDF量子化学计算软件正式商用

1993年到2022年
精雕细琢
“三十年磨一剑”
定位于发展新理论、新方法和新算法的平台
BDF这款量子化学计算软件
终于正式商用!
这是国产科学计算软件的发展之路
也是研发人员与用户的共进之路
更是基础理论研究的演变史
让我们走近它
一起了解BDF的发展历程
一起体验BDF独具特色的功能
BDF (Beijing Density Functional) 是一款独立完整、特色鲜明、具有完全自主知识产权的量子化学计算软件包,尤其擅长重元素体系电子结构计算。
BDF软件的发展史
1、 最初的想法
对稀土、锕系、过渡金属、超重元素等小分子体系进行高精度计算,考察这些体系中的相对论效应。
2、 采用的理论
基于Dirac算符的完全相对论密度泛函理论(4C-DFT)和近乎完备的基函数“数值基+STO”(Slater-type orbital)
3、取得的成就
BDF对稀土、锕系、超重元素的计算结果一直被作为检验其他近似相对论方法的基准。BDF对重元素体系电子、分子结构的计算结果被后续20余个实验验证。
引入基于高斯基的解析积分
开启基础理论发展的新篇章
基于BDF发展的理论、方法和算法
相对论含时密度泛函理论(4C/ZORA/X2C-TDDFT)[2-7]
精确二分量(X2C)相对论理论[8-10]
准四分量(Q4C)相对论理论[10,11]
自旋分离的X2C相对论理论(sf-X2C+so-DKHn)[12,13]
多体有效量子电动力学(eQED)[14,15]
相对论核磁理论(4C/X2C-NMR)[16-23]
相对论核自旋-转动理论(4C-NSR)[23-25]
相对论能带理论(X2C-PBC)[26]
X2C解析梯度和Hessian[27]
激发态HF/KS方法(mom)[28]
基于“用分子片合成分子” (F2M)思想的轨道局域化方案(FLMO)[28-30]
亚线性标度含时密度泛函理论(FLMO-TDDFT)[31]
亚线性标度NMR方法(FLMO-NMR)[32]
迭代轨道相互作用 “自下而上”自洽场方法(iOI)[33]
自旋匹配开壳层含时密度泛函理论(SA-TDDFT)[34-38]
自旋反转含时密度泛函理论(SF-TDDFT)[39]
基态/激发态-激发态非绝热耦合含时密度泛函理论(NAC-TDDFT)[40-42]
含时密度泛函理论解析能量梯度[43]
任意单值/双值点群对称化[44]等
除了上述相对论/非相对论密度泛函、含时密度泛函理论,BDF还有基于“先静态再动态又静态”(SDS)思想的波函数电子相关方法SDSPT2[45]、SDSCI[45]、iCI[46]、iCIPT2[47,48]、iCAS[49]、iCISCF[50]、SOC-iCI、iCI-SOC,以及直接求解大矩阵内部本征态的iVI方法[51,52]等等。
鉴于BDF的现状,首期商业化版本将以荧/磷光材料发光机理和材料设计为主要应用目标,因此不包括4C/X2C相对论、波函数电子相关、固体能带/核磁等方法。
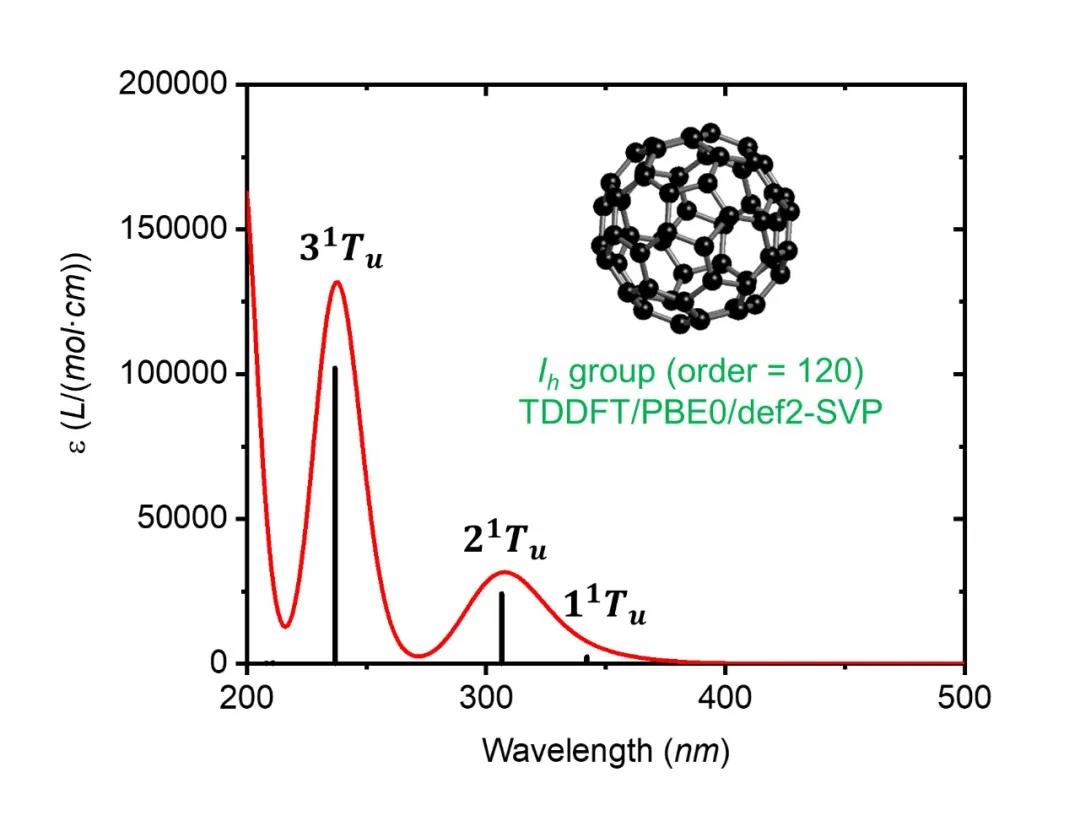
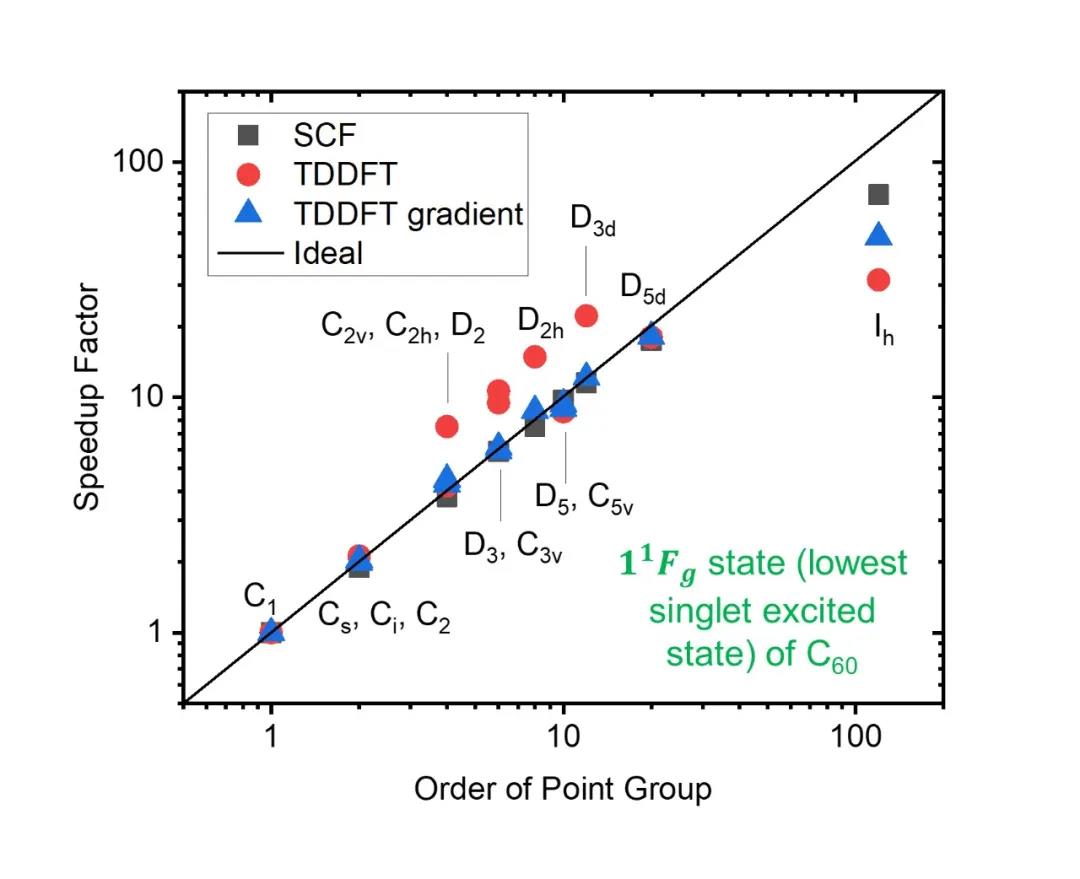
首期商业化的BDF将以DFT、TDDFT为主,包括基态与激发态KS、QM/MM、FLMO-TDDFT、SF-TDDFT、NAC-TDDFT、sf-X2C-SA-TDDFT/SOC、SA-TDDFT解析能量梯度和数值Hessian、稳定结构和过渡态优化、反应路径优化、隐式溶剂化模型、FLMO-NMR、基于局域轨道(FLMO)的性质计算和分析等特色功能。
※※※
| 联系我们了解试用BDF软件 |
marketing@hzwtech.com
sales@hzwtech.com
support@hzwtech.com
鸿之微小助手微信:hzwtech-1
QQ群:452912262
试用链接:https://iresearch.net.cn/mobile/trialForm?productId=13
1) W. Liu, G. Hong, D. Dai, L. Li, and M. Dolg, The Beijing 4-component Density Functional Program Package (BDF), Theoretical Chemistry Accounts 96 (1997) 5-83.
2) J. Gao, W. Liu, B. Song, and C. Liu, Time-dependent Four-component Relativistic Density Functional Theory for Excitation Energies, J. Chem. Phys. 121 (2004) 6658-6666.
3) J. Gao, W. Zou, W. Liu, Y. Xiao, D. Peng, B. Song, and C. Liu, Time-dependent four-component relativistic density-functional theory for excitation energies. II. The exchange-correlation kernel, J. Chem. Phys. 123 (2005) 054102-13.
4) D. Peng, W. Zou, and W. Liu, Time-dependent quasirelativistic density functional theory based on the zeroth-order regular approximation, J. Chem. Phys. 123 (2005) 144101.
5) W. Xu, J. Ma, D. Peng, W. Zou, W. Liu, and V. Staemmler, Excited states of ReO4-: A comprehensive time-dependent relativistic density functional theory study, Chem. Phys. 356 (2009) 219-228.
6) W. Xu, Y. Zhang, and W. Liu, Time-dependent relativistic density functional study of Yb and YbO, Sci. China Chem. 52 (2009) 1945-1953.
7) Z. Li, B. Suo, Y. Zhang, Y. Xiao, and W. Liu, Combining spin-adapted open-shell TD-DFT with spin-orbit coupling, Mol. Phys. 111 (2013) 3741-3755.
8) W. Kutzelnigg and Wenjian Liu, Quasirelativistic theory equivalent to fully relativistic theory, J. Chem. Phys. 123 (2005) 241102.
9) W. Liu and D. Peng, Exact two-component Hamiltonians revisited, J. Chem. Phys. 131 (2009) 031104.
10) W. Liu and D. Peng, Infinite-order quasirelativistic density functional method based on the exact matrix quasirelativistic theory, J. Chem. Phys. 125 (2006) 044102.
11) D. Peng, W. Liu, Y. Xiao, and L. Cheng, Making four-and two-component relativistic density functional methods fully equivalent based on the idea of ''from atoms to molecule'', J. Chem. Phys. 127 (2007) 104106.
12) Z. Li, Y. Xiao, and W. Liu, On the spin separation of algebraic two-component relativistic Hamiltonians, J. Chem. Phys. 137 (2012) 154114.
13) Z. Li, Y. Xiao, and W. Liu, On the spin separation of algebraic two-component relativistic Hamiltonians: Molecular Properties, J. Chem. Phys. 141 (2014) 054111.
14) W. Liu and I. Lindgren, Going beyond'no-pair relativistic quantum chemistry', J. Chem. Phys. 139 (2013) 014108.
15) W. Liu, Advances in relativistic molecular quantum mechanics, Phys. Rep. 537 (2014) 59-89.
16) Y. Xiao, D. Peng, and W. Liu, Four-component relativistic theory for nuclear magnetic shielding constants: The orbital decomposition approach, J. Chem. Phys. 126 (2007) 081101.
17) Y. Xiao, W. Liu, L. Cheng, and D. Peng, Four-component relativistic theory for nuclear magnetic shielding constants: Critical assessments of different approaches, J. Chem. Phys. 126 (2007) 214101.
18) L. Cheng, Y. Xiao, and W. Liu, Four-component relativistic theory for NMR parameters: Unified formulation and numerical assessment of different approaches, J. Chem. Phys. 130 (2009) 144102.
19) L. Cheng, Y. Xiao, and W. Liu, Four-component relativistic theory for nuclear magnetic shielding: Magnetically balanced gauge-including atomic orbitals, J. Chem. Phys. 131 (2009) 244113.
20) Q. Sun, W. Liu, Y. Xiao, and L. Cheng, Exact two-component relativistic theory for nuclear magnetic resonance parameters, J. Chem. Phys. 131 (2009) 081101.
21) Q. Sun, Y. Xiao, and W. Liu, Exact two-component relativistic theory for NMR parameters: General formulation and pilot application, J. Chem. Phys. 137 (17) (2012) 174105.
22) Y. Xiao, Y. Zhang, and W. Liu, New experimental NMR shielding scales mapped relativistically from NSR: Theory and application, J. Chem. Theor. Comput. 10 (2014) 600-608.
23) Y. Xiao and W. Liu, Body-fixed relativistic molecular Hamiltonian and its application to nuclear spin-rotation tensor: Linear molecules, J. Chem. Phys. 139 (2013) 034113.
24) Y. Xiao and W. Liu, Body-fixed relativistic molecular Hamiltonian and its application to nuclear spin-rotation tensor, J. Chem. Phys. 138 (2013) 134104.
25) Y. Xiao, Y. Zhang, and W. Liu, Relativistic theory of nuclear spin-rotation tensor with kinetically balanced rotational London orbitals, J. Chem. Phys. 141 (2014) 164110.
26) R. Zhao, Y. Xiao, Y. Zhang, and W. Liu, Exact two-component relativistic energy band theory and application, J. Chem. Phys. 144 (2016) 044105.
27) W. Zou, G. Guo, B. Suo, and W. Liu, Analytic energy gradients and Hessians of exact two-component relativistic methods: Efficient implementation and extensive applications, J. Chem. Theory Comput. 16 (2020) 1541-1554.
28) J. Liu, Y. Zhang, and W. Liu, Photoexcitation of light-harvesting C-P-C60 triads: A FLMO-TD-DFT Study, J. Chem. Theory Comput. 10 (2014) 2436-2448.
29) F. Wu, W. Liu, Y. Zhang, and Z. Li, Linear scaling time-dependent density functional theory based on the idea of ''from fragments to molecule'', J. Chem. Theor. Comput. 7 (2011) 3643-3660.
30) Z. Li, H. Li, B. Suo, and W. Liu, Localization of molecular orbitals: From fragments to molecule, Acc. Chem. Res. 47 (2014) 2758-2767.
31) H. Li, W. Liu, and B. Suo, Localization of open-shell molecular orbitals via least change from fragments to molecule, J. Chem. Phys. 146 (2017) 104104.
32) M. Yuan, Y. Zhang, Z. Qu, Y. Xiao, and W. Liu, Sublinear scaling quantum chemical methods for magnetic shieldings in large molecules, J. Chem. Phys. 150 (2019) 154113.
33) Z. Wang and W. Liu, iOI: An iterative orbital interaction approach for solving the self-consistent field problem, J. Comput. Theory Comput. 17 (2021) 4831-4845.
34) Z. Li and W. Liu, Spin-adapted open-shell random phase approximation and time-dependent density functional theory. I. Theory, J. Chem. Phys. 133 (2010) 064106.
35) Z. Li, W. Liu, Y. Zhang, and B. Suo, Spin-adapted open-shell time-dependent density functional theory. II. Theory and pilot application, J. Chem. Phys. 134 (2011) 134101.
36) Z. Li and W. Liu, Spin-adapted open-shell time-dependent density functional theory. III. An even better and simpler formulation, J. Chem. Phys. 135 (2011) 194106.
37) Z. Li and W. Liu, Critical assessment of TD-DFT for excited states of open-shell systems: I. Doublet-doublet transitions, J. Chem. Theory Comput. 12 (2016) 238-260.
38) Z. Li and W. Liu, Critical assessment of TD-DFT for excited states of open-shell systems: II. Doublet-quartet transitions, J. Chem. Theory Comput. 12 (2016) 2517-2527.
39) Z. Li and W. Liu, Theoretical and numerical assessments of spin-flip time-dependent density functional theory, J. Chem. Phys. 136 (2012) 024107.
40) Z. Li and W. Liu, First-order nonadiabatic coupling matrix elements between excited states: A Lagrangian formulation at the CIS, RPA, TD-HF, and TD-DFT levels, J. Chem. Phys. 141 (2014) 014110.
41) Z. Li, B. Suo, and W. Liu, First order nonadiabatic coupling matrix elements between excited states: Implementation and application at the TD-DFT and pp-TDA levels, J. Chem. Phys. 141 (2014) 244105.
42) Z. Wang, C. Wu, and W. Liu, NAC-TDDFT: Time-Dependent Density Functional Theory for Nonadiabatic Couplings, Acc. Chem. Res. 54 (2021) 3288-3297.
43) Z. Wang, Z. Li , Y. Zhang, and W. Liu, Analytic energy gradients of spin-adapted open-shell time-dependent density functional theory, J. Chem. Phys. 153 (2020) 164109.
44) D. Peng, J. Ma, and W. Liu, On the construction of Kramers paired double group symmetry functions, Int. J. Quantum Chem. 109 (2009) 2149-2167.
45) W. Liu and M. R. Hoffmann, SDS: the 'static-dynamic-static' framework for strongly correlated electrons, Theor. Chem. Acc. 133 (2014) 1481.
46) W. Liu and M. R. Hoffmann, iCI: Iterative CI toward full CI, J. Chem. Theory Comput. 12 (2016) 1169-1178.
47) N. Zhang, W. Liu, and M. R. Hoffmann, Iterative configuration interaction with selection, J. Comput. Theory Comput. 16 (2020) 2296-2316.
48) N. Zhang, W. Liu, and M. R. Hoffmann, Further development of iCIPT2 for strongly correlated electrons, J. Comput. Theory Comput. 17 (2021) 949-964.
49) Y. Lei, B. Suo, and W. Liu, iCAS: Imposed Automatic Selection and Localization of Complete Active Spaces, J. Comput. Theory Comput. 17 (2021) 4846-4859.
50) Y. Zhang, B. Y. Guo, N. Zhang, Y. Lei, and W. Liu, iCISCF: An Iterative Configuration Interaction-Based Multiconfigurational Self-Consistent Field Theory for Large Active Spaces, J. Chem. Theory Comput, J. Chem. Theory Comput. 17(2021)7545?7561 .
51) C. Huang, W. Liu, Y. Xiao, and M. R. Hoffmann, iVI: an iterative vector interaction method for large eigenvalue problems, J. Comput. Chem. 38 (2017) 2481-2499; (E) 39 (2018) 339.
52) C. Huang and W. Liu, iVI-TD-DFT: An iterative vector interaction method for exterior/interior roots of TD-DFT, J. Comput. Chem. 40 (2019) 1023-1037.
你可能感兴趣



技术支持
鸿之微科技(上海)股份有限公司愿 竭力为用户和企业提供全方位的技 术支持和服务。








